Before The Web: Computation and Cybernetics in Astounding Science Fiction, May, 1949 – “Electrical Mathematicians”

From Astounding Science Fiction of May, 1949, the article “Electrical Mathematicians,” by Lorne Maclaughlan, focuses on the the use of computers – specifically, electronic as opposed to purely mechanical computers – as devices to perform mathematical calculations.  It’s one of the four non-fiction articles pertaining to cybernetics and computation published by the magazine that year, the other three having been:

“Modern Calculators” (digital and analog calculation), by E.L. Locke; pp. 87-106 – January

“The Little Blue Cells” (‘Selectron’ data storage tube), by J.J. Coupling; pp. 85-99 – February

“Cybernetics” (review of Norbert Wiener’s book by the same title), by E.L. Locke; pp. 78-87 – September

The identity and background of author Maclaughlan remain an enigma.  (At least, in terms of “this” post!)  The Internet Speculative Fiction Database shows only two other entries under his name, both in Astounding (“Noise from Outside” in 1947, and “Servomechanisms” in 1948, while web searches yield a parallel paucity of results.  This absence biographical information, especially in light of the over seven decades that have transpired since 1949, coupled with the author’s distinctive writing style – combining clarity and economy of expression, and, an ease and familiarity with the language of technology – leads me to wonder if that very name “Lorne Maclaughlin” (note the lack of a middle initial?) might actually have been a pen-name for an engineer or academic.  Given the somewhat ambiguous reputation of science-fiction in professional and credentialed circles (albeit a reputation by the 1940s steadily changing for the better) maybe “Maclaughlan” – assuming the name was a pseudonym – might have wanted to maintain a degree of anonymity. 

Well, if so (maybe so?!) that anonymity has successfully persisted to this day!  

Anyway, the cover art’s cool. 

Depicting a scene from the opening of Hal Clement’s serialized novel Needle (the inspiration for the 1987 Kyle MacLachlan film The Hidden?), it’s one of the three (color, naturally) Astounding Science Fiction cover illustrations by Paul Orban, an illustrator primarily known for interior work, whose abundant output was only exceeded by his talent. 

As for Maclaughlan’s article itself, it begins with a brief overview of the implications of the increasing centrality of calculating devices in contemporary (1949 contemporary, that is!) society, and the future.

This is followed by a discussion of the very nature of calculation, whether performed by mechanical or electronic devices, which then segues into a comparison of the similarities and differences between binary and decimal systems of counting and computation, and an explanation of the utility of the former in computing devices.

Next, a lengthy discussion of memory.  (We’ve all heard of that…)  note the statement, “Not only must we “teach” the machine the multiplication table – by the process of wiring in the right connections – but it may also be necessary to provide built-in tables of sine and cosine functions, as well as other commonly used functions.  This is a permanent kind of memory – a fast temporary kind of memory is also needed to remember such things as the product referred to above until it is no longer needed.  This memory has not been easy to provide in required amounts, but recently invented electronic devices seem to offer some hope that this difficulty can be overcome.”  In this, author Maclaughlan is anticipating what we know today as ROM (read-only-memory) and RAM (random-access-memory), respectively.  This is followed by the topic of data input and manipulation, in the context of Hollerith Cards and Charles Babbage’s “Difference Engine”.  (For the latter, see “Babbage’s First Difference Engine – How it was intended to work,” and, “The Babbage Engine,” the latter at Computer History Museum.

From this, we come to computation in terms of the technology and operation of then-existing computers.   This encompasses ENIAC (Electronic Numerical Integrator and Computer), EDVAC (Electronic Discrete Variable Automatic Computer), and MANIAC (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I), and briefly touches upon the Selectron tube, the latter device the subject of J.J. Coupling’s article in the February 1949 issue of Astounding.

The final part of Mclaughlan’s article is a discussion of the nature, advantages, and use of “analyzers” – Differential Analyzers, and Transient Network Analyzers – in computation:  Specifically, in the solution of differential equations pertinent to scientific research, such as, “…the flow of microwave energy in wave-guides, the flow of compressible fluids in pipes, and even the solution of Schrodinger’s Wave Equation,” or military applications, such as aiming anti-aircraft guns or determining the trajectory of nuclear weapons, noting, “These latter-day buzz-bombs will be sufficiently lethal to warrant their carrying along their own computers.” 

Prescience, or, inevitability?  

And finally, the article concludes with a photograph.  

And, so…

ELECTRICAL MATHEMATICIANS

“The differential analyzer is more versatile than the network analyzer discussed above because it can integrate, differentiate – in effect – and multiply, and thus solve rather complicated differential equations.  These functions are performed by mechanical or electro-mechanical devices in the differential analyzer.  If these things could be accomplished by purely electrical means, we would expect a great increase in speed, and some decrease in size and weight.”  

To an extent none of us today can realize, these rapidly growing electrical calculators will become more and more important factors in ordinary life.  So far, they are handling only simple, straight-arithmetic problems.  They are brains, but so far they think only on low levels.  Give them time; they will be planners yet!

In this machine age no one is surprised at the announcement of some new or improved labor-saving device.  The scientists and technologists who design our new electronic rattraps, microwave hot-dog dispensers and atomic power plants have succeeded so well that they have created a serious manpower shortage in their own professions.  This shortage, which is chiefly in the field of analysis has recently forced them to put an unprecedented amount of effort into the design of machines to save themselves mental labor.  The results of their efforts are an amazingly variegated collection of computing machines, or “artificial brains” as they are called in the popular press:

The development of such machines took a tremendous spurt during the war, and today we can scarcely find a laboratory or university in the land which is not devoting some part of its efforts to work of this kind.  Progress is so rapid that the machines are obsolete before they are completed, and thus no two identical machines exist.

We cannot say that the computing machine is a new invention – the unknown Chinese originator of the abacus provided man with his first calculating machine in the sixth century B.C.  This would seem to make the machine nearly as old as the art of calculating, but man is equipped with fingers and toes which have always provided a handy portable computing device.  In fact, as we shall see, the simple fact that we have ten lingers has a definite bearing on the number of tubes and the kind of circuits required in electronic digital computers.

__________

 

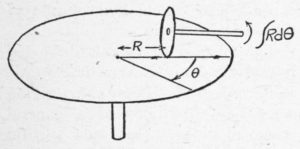
Kelvin Wheel-and-Disk integrator.  This device, which gives the integral of a radial distance with respect to an angle, is the most important unit in a differential analyzer of the electromechanical type.

__________

It should be pointed out that there are two distinct types of computing machines in common use today.  One type deals with discrete whole numbers, counting them off with the aid of teeth on a wheel, or electrical pulses in vacuum tube circuits.  These numbers represent quantities, and they are added and multiplied just as numbers are on paper, but at a much higher speed.  These machines called digital computers, range from the simple cash-register adding machine to the complex all-electric ENIAC, with its eighteen thousand radio-type vacuum tubes.

The other type of machine is the analogue type of computer, in which the number to be dealt with is converted into some measurable quantity, such as length along a slide rule, or angle of rotation of a shaft.  The operations are performed electrically or mechanically, and the answer appears as a length, an angle, a voltage or some other quantity which must be converted back to a number.  The ideal machine of the analogue type will accept mathematical functions, empirical curves and directions for mixing and stirring, and turn out results in the form of curves automatically.

The digital computer is much more accurate than the analogue type for the simple reason that is easy to extend the number of significant digits in such machines to something like thirty or forty.  It is impossible to measure a point on a curve to anything approaching one part in 1040.  However, the analogue computers are in many ways faster and more versatile, because they can perform certain difficult mathematical operations directly, while digital machines require that these operations be reduced to addition and multiplication.

One of the first things we must do to understand modern digital computing machines is to disconnect our minds from the decimal number system, and get a more basic concept of number representation.  The decimal system of numbers is a natural choice, based on the fact man has that ten fingers.   We would perhaps be more fortunate had evolution given us twelve, for then our number system would be the more convenient duo-decimal system.  Let us examine this system as a starting point, by studying the table of numbers below.

1 2 3 4 5 6 7 8 9 * t 10
11 12 13 14 15 16 17 18 19 1* t 20
21 22 23 24 25 26 27 28 29 2* t 30

The six-fingered man would count to six on one hand, and then continue, seven, eight, nine, star, dagger, ten on the other.  His ten would be our twelve, of course, but it would be a resting point for him while he got his shoes off to continue to his twenty – our twenty-four – on his twelve toes.

If we continue the table for twelve lines of twelve numbers each we will get to his one hundred, which corresponds to our one hundred forty-four.  This number is his ten squared – our twelve squared – as it would be, and is preceded by his daggerty-dagger, ††.  This duodecimal system has the advantage that ten can be divided by 2, 3, 4 and 6, giving in each case whole numbers – 10/4 = 3, 10/6 = 2, et cetera – while our ten is only divisible by 2 and 5.  The ancient Babylonians were fond of this system, and also used sixty as a number base.  These systems remain today as the bases of our measurement of time in seconds, minutes and hours.

Now let us examine the binary system, based on two.  In this system all numbers are made up of combinations of just two digits, one and zero.  The simplicity of this system makes it possible to use simple devices such as electromagnetic relays to represent numbers.  The simple relay has two possible positions, open and closed, and we can represent zero by means of the open position, and one by the closed position, and then build up any number as shown in the table below.

Decimal System Binary System
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010

Computation is easy with this system, once we get the hang of it.  Thus our two cubed becomes, 1011 = 10 x 10 x 10 = 1000, and our two times three becomes 10 x 11 = 110, which is our six, as it should be.

With our minds cleared for action on any number base let us consider the capabilities which are necessary in a digital computer.  Digital computation requires that all operations be reduced to those of addition, subtraction, multiplication and division whether a machine is used or not.  These operations involve certain reflex actions, such as the response “six” when presented with the numbers “two” and “three” and the idea “multiply.”  The trained human mind possesses such reflex actions, and the machine must also possess them, as a first requirement.  Simple computing devices such as the commercial accounting machine possess a few reflexes.  It is necessary to build many rapid reflexes into mathematical computing machines.

The next “mental” capability the machine must possess is that of memory.  When we must multiply two numbers together before adding them to a third, memory is needed to preserve the product until the second operation can be performed.  Commercial calculating machines have limited memory – after multiplication, for example, the number appears on the output wheels, and the third number can easily be added.  The memory requirements in a good mathematical machine are much, much more stringent, and provide some of the toughest problems in design.  Not only must we “teach” the machine the multiplication table – by the process of wiring in the right connections – but it may also be necessary to provide built-in tables of sine and cosine functions, as well as other commonly used functions.  This is a permanent kind of memory – a fast temporary kind of memory is also needed to remember such things as the product referred to above until it is no longer needed.  This memory has not been easy to provide in required amounts, but recently invented electronic devices seem to offer some hope that this difficulty can be overcome.

There are still two capabilities left.  These are choice and sequence.   The computing machine should be able to choose between two numbers, or two operations it can perform, in accordance with certain rules.  Sequence involves, as the name implies, the proper choice of order of numbers or operations according to some rule which applies in the particular problem being solved.

These last two capabilities are not found to any great extent in any but the most modern mathematical computing machines.  On the other hand there are a multitude of other mental capabilities found in humans which are undesirable in mathematical machines.  Emotion, aesthetics, creative ability and so forth are not desirable, for these help to make humans unfit for much routine computing work.  What we want is perfect slave, fast, untiring and industrious, who will never embarrass or disconcert us with unexpected response.  (Of course the engineers in charge of some of the complicated modern mathematical machines are quick to accuse them of temper tantrums and other undesirable emotions.)

Perhaps the fanciest digital computing machine today is the IBM Automatic Sequence Controlled calculator at Harvard.  The letters IBM International Business Machines Corporation, which has developed a series of machines intended for use in accounting work.  These machines use a punched card – a device with quite a history, as histories go in the computing field.  It would seem that weaving machines which could be used to more or less automatically weave patterned cloth excited the imagination of a good many inventors in in the early eighteenth century.  In such weaving it was necessary to sequence automatically the “shredding,” or controlling of the warp threads so that weft threads could be passed through them to weave a pattern.  Punched tape and punched cards had already been by 1727.  The punched cards we use today get the name Jacquard cards from the name of the inventor of an improved weaving machine around the year 1800.

This basic idea was good enough to attract the attention of Charles Babbage, an English actuary, who is regarded as the lather of the modern computing machine.  His “difference engine” was designed, in his words, “to perform the whole operation” – of the computing and printing of tables of functions – “with no mental attention when numbers have once been fed in the machine.”  When this “engine” was nearly complete the government withdrew its support of the Project, and Babbage began the construction of an analytical machine on his own.  This machine, a wholly mechanical device, was to use punched Jacquard cards for automatic sequencing.  In 1906 his son successfully completed a machine with which he calculated pi to twenty-nine significant figures.

Hollerith, in this country, made a great advance in the use of punched cards when he invented a card sorter to aid in classifying the results of the 1880 census.  Most people today are familiar with the kind of things that a sorter can do.  Thus if we have a sorter and a stack of cards with personal and alphabetical information punched thereon we can request the machine to pick out all left-handed individuals with cross-eyes and Z for a second initial, and bzzzzt, bzzzzt, bzzzzt – there they are.

The IBM Company, by catering to the needs of organizations which handle – and have – a good deal of money, was able to put the manufacture of computing machines on a paying basis.  It need not be pointed out that it is much more difficult to produce profitably machines which will only be used for such tasks as the calculation of pi to umpteen places.  However the punched card machines built for accountants have found their way into scientific computing laboratories, and the IBM Company has a research laboratory which is actively developing new machines for scientific use as well as for accounting.

A punched card machine operating on the Hollerith principle interprets numerical and operational data according to the positions of holes punched on cards, and then perform various mathematical operations.  The cards, which are familiar to most people – postal notes, government checks, et cetera – have twelve vertical positions in each of eighty columns.  The vertical positions are labeled y, x, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.  Thus an 80 digit or two 40 digit numbers can be set up on one card, and the y space, for example, may be used to indicate sign.

The cards are read for purposes of sorting et cetera by a simple mechanism involving a metal cylinder and sets of electrically conducting brushes.  As the card moves between the rotating cylinder and the eighty brushes, one for each column, an electrical contact is made whenever a punched hole passes under a brush.  The position of the cylinder at the time that the brush makes contact indicates the number, or letter, represented.  Any number system could be used, but the decimal system is selected because of its familiarity.  The various IBM machines now on the market include Card Punchers, Card Interpretaters [sic], Card Sorters, Collators and others, all operating on the same basic principles.  The most useful machine to scientific workers is the Automatic Multiplying Punch.  This machine will multiply factors punched in cards, and will automatically punch the product in a card, or even add and punch out products.

The computer lab at Harvard, mentioned above, uses a combination of these machines and a device for sequencing their operations – whence the name IBM Automatic Sequence Controlled.  This calculator is one of the half-dozen large machines in this country which can be used to tear into a tough problem and quickly reduce it to a neat column of figures – or a stack of cards, in this case.  Since it is a digital type of computer capable of great accuracy, but because it is partly mechanical in operation it is slow compared to the newer all electronic machines.  The automatic sequencing apparatus is not easy to set up, and thus type of machine is best suited to the solution of repetitive types of problems, such as the calculation of tables.  The punched card is a convenient form in which to store tables of simple functions, e.g. Sin x, Log x, which are often needed in computation of tables of more complicated functions.

Of course, if you want to prepare a table umpteen places Bessell Functions, or evaluate some determinants, or make some matrix algebra manipulations you will have to wait s time for your turn on this or any similar machine.  You will have to have a pretty good story too, for these machines are at work today, and sometimes night as well with important problems.  It must be realized too, that a problem be rather important and complex before it is even worthwhile to the labor of setting it up for solution in such a complicated machine.

Punched cards are often used to store scientific data other than tables with the advantages of machine sorting et cetera possible with IBM machines.  Thus at the Caltech wind tunnel data from instruments is punched directly on cards.  Astronomers locate star images by pre-computed co-ordinates on punched cards, and then measure the star positions accurately and record the new information on new cards.  The Census Bureau makes a great deal of use of punched cards at present, but plans are being made to go over to the faster electronic computers for this work.

__________

 

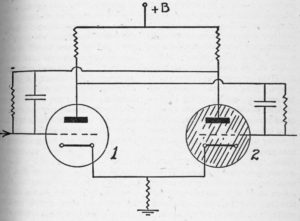
Basic flip-flop vacuum-tube circuit used in the ENIAC and in other digital computers.  Tube number 2 – shaded – is conducting, and tube number 1 is “cut-off”, in the diagram above.  A positive pulse on tube 1 will cause it to conduct and the resultant drop in its plate voltage will cause tube 2 to cease conducting.  This condition is stable until another pulse arrives, on the grid of tube 2.  

__________

Shortly before the war, G.R. Stibitz and others at the Bell Telephone Laboratories developed a relay type of computer which could handle not only real numbers but complex numbers as well.  The binary number system is convenient in a relay computer as we have pointed out.  There is some difficulty entailed in the process of getting from a number expressed in the ordinary decimal system to the binary system and back again.  For this reason Stibitz likes what he calls a bi-quinary system, which uses base 2 to tell if a number is between 0 and 4, or 5 and 9, and base 5 to tell which digit it is of the five.  Early in the war the Army and Navy each ordered one of these relay computers, and machine computation was off to a flying start.

Dr. H.H. Aiken, who had built the IBM computer at Harvard has recently gone over to the relay type of computer, and his “Mark II” will soon be in operation on the complicated guided missile ballistics problems being studied at the Dahlgren Proving Ground.  IBM has also been playing around with relay computers, and has delivered two sequence controlled machines of this type for ballistic research workers.  Aiken does his sequencing with standard teletype tape, while some of the IBM jobs use plugboards.

An interesting example of a similar parallel development is the Zuse computer, named after its designer Conrad Zuse, who developed his machine in Germany during and since the war.  Like the Bell Laboratories machine it uses a keyboard to feed numbers into its relays.  The sequence is prepared in advance by an operator who punches instructions into a strip of film.

The art of machine computation took a tremendous jump ahead when in the fall of 1946 the ENIAC, the first electronic digital machine, was placed in operation.  This machine was built for Army Ordnance at the Moore School of Engineering by J.W. Mauchly, J.P. Eckert and others.  The ENIAC – Electro Numerical Integrator and Calculator – with its eighteen thousand tubes is over a thousand times faster than the relay machines, which in turn were twelve times faster than the original punched card machine at Harvard.  This tremendous increase in speed is the result of shifting over from the use of one gram relay armatures to the use of 10-31 gram electrons as moving parts.  Of course a number of new problems appeared when this one limitation was removed.  They are being cleared up one by one, chiefly by electronic means.

The ENIAC, despite the light weight of its moving parts, is no vest-pocket machine, as the number of vacuum tubes would indicate.  The filaments of these tubes alone require eighty kilowatts of power, and a special blower system is needed to take away the heat.  The whole machine occupies a space about 100 feet by 10 feet by 3 feet.  Tube failures were a source of a good deal of trouble, because for while at least one of the eighteen thousand tubes burned out each time the power was turned on.  This trouble was reduced by leaving the filaments of the tubes on, night and day, to eliminate the shocks involved in heating and cooling, so that now the ENIAC burn-outs at only about one per day, which take on the average of only fifteen minutes to repair.  Experience with this machine has aided the design of a series of successors, such as the EDVAC, the UNIVAC, and the MANIAC – inevitable name.

The most important type of unit in the ENIAC is a device which uses two triode tubes, called a flip-flop circuit.  These tubes will do electrically what the relay does mechanically.  Normally one of the two tubes is conducting current, and the other is “cut off.” A very short – 0.000001 seconds long – pulse of voltage can cause this tube to cut off or cease to conduct, and the other to begin to conduct.  Since only these two stable states are possible, we have the beginning of a binary computer.  We must add a small neon bulb to indicate when the second tube is conducting, and then add as many such units in series as there are binary digits in the number we wish to handle.  These circuits are used as a fast memory device.  The ENIAC has a fast memory of only twenty ten-digit numbers, a serious limitation which can only be overcome by adding to the already large lumber of tubes, or by going to other types of fast memory.

Adding is accomplished by connecting flip-flop circuits in tandem so that they can count series of electrical pulses.  This counting works in the same way that the mileage indicator works in a car, except that the scale of two is used.  Thus, suppose that initially all our flip-flop circuits are in one condition – call it flip.  The first pulse causes the first circuit to go from flip to flop.  The next one will return it to flip, and this causes the first circuit to emit a pulse which sends the second circuit to flop.  This continues on throughout the chain of circuits, all connected in tandem, as long as pulses are fed into the first circuit.  When two series of pulses have been fed in we can get our number by noting which circuits are on flip – binary zero – and which on flop – binary one.  The result may be converted back to pulses for use elsewhere.  The speed per digit in the adding operation is a comfortably short ten microseconds.

The description of the adding scheme above has omitted one added complication in circuit design which gives a considerable simplification in reading of numbers.  The binary system is used to count only to ten in the ENIAC and the number is then converted to a decimal number.  This is a bit of a nuisance, circuit-wise, but handy – the decimal system is familiar.

The ENIAC also has electronic circuits for multiplying, dividing, square-rooting and so forth.  The multiplier uses a built-in electrical multiplication table to aid it in its high-speed, ten digit operation.  One very important unit in the ENIAC is the master programmer, which changes the machine from one computing sequence to another, as a complex computation progresses, in accordance with a pre-set plan.  The master programmer even makes possible connections which enable the machine to choose the proper computing sequence when faced with the necessity for a choice.  Thus it would almost seem that the machine does possess a kind of built-in judgment, and that there is some reason for the term “electrical brain.”

It was mentioned that the fast memory of the ENIAC was limited.  The slow memory, using punch cards, and IBM machines causes a great reduction in speed when it must be used.  Also, although computation is all-electronic, data is fed in and results are taken out by electromechanical means – punch cards again.  The limitations incurred may best be realized if we compare the time for a punch, about half a second, with the unit time of a flip-flop circuit, ten microseconds.  The ratio is fifty thousand times.

Even more serious is the problem common to all digital machines, namely the difficulty of setting up a problem.  These machines are not easy to use, and the sequence of operations for an easy problem may be very involved.  If the problem is difficult, then, of course, the sequence gets more difficult, but the use of machine methods is mandatory.  So, when faced with a real stinger of a problem, the scientist gets down to work, perhaps for months, just to figure out how to set up the machine.  Considerable time is needed for the physical setting up of sequence connections too, but after that – brrrrrrrrrrrrrp, and a solution which would take years by former methods begins to roll out in a matter of minutes.

Professor D.R. Hartree of England, who recently worked with the ENIAC, describes the solution of problem in which this machine had to handle two hundred thousand digits.  Now try writing digits as fast as possible.  At a rate which will lead to errors and writer’s cramp you may put down ten thousand digits in an hour.  Even at this speed it will take twenty hours just to write down two hundred thousand digits – and no computation has been performed.  The machine handled the numbers and performed the computation in this example in four minutes flat.  It is not surprising that Professor Hartree is impressed by such speeds – he once spent fifteen years on the computation of the electron orbits of atoms.  This is the kind of job that a machine calculator can be coerced into doing in a few hours, or days at most.

Their utility to science is obvious!

The ENIAC is only the first of its kind.  The EDVAC – Electronic Discrete Variable Computer – is an improved machine, also built Army Ordnance at the r of Pennsylvania.  One of the chief improvements is a larger capacity memory device, made possible use of acoustical delay lines for storage of numbers.  Numbers get stored as trains of compression pulses is bouncing back and forth in a two-inch column of mercury.  Each delay line of this type does the work of five hundred fifty electronic tubes in the ENIAC, so that a substantial saving results.

The MANIAC – Mechanical and Numerical Integrator and Computer – is another Army Ordnance computer.  It is being built at the Institute of Advanced Study at Princeton under the direction of Dr. J. von Neumann and Dr. H.H. Goldstine.  This machine is to use a new type of fast memory tube which is being perfected by Dr. Jan Rajchman of RCA.  This tube, called the Selectron, is a kind of cathode ray tube which is designed to store four thousand ninety-six off-on or binary signals – equivalent to about twelve hundred decimal digits.  The binary digits are to be stored as charge on points on a cathode screen which are behind the interstices of two orthogonal sets of sixty-four wires each.  An ingenious method of connecting certain of these wires together will enable electric signals to be fed in to pull the electron beam to any position for purposes of reading” or “writing” with just thirty-two leads brought out.  Even so a pre-production model of the tube looks a bit formidable, but it is phenomenally small for the memory it possesses.

Among some of the other schemes for digital memory being worked on are delay networks using loops of wire in wire recorders.  This scheme may not be as fast as the acoustical delay line used in the EDVAC, but it has the advantage that the pulses do not have to be periodically removed for reshaping.  One practical difficulty here is the necessity of waiting for the right point on the wire to come around before reading begins.  Of course all memory of a number can easily be erased when need for it is finished, and the wire loop is ready to be re-used.

It seems that the Selectron is one of the best bets to speed up the operation of all-electronic computers.  With its aid it should be possible to multiply two twelve-digit numbers in one hundred millionths of a second.

Such speeds may seem fantastic, but problems have been formulated and shelved because even the fastest present-day computing machines could not complete the solution in thousands of years.

The Bureau of Standards, aided by Mauchly and Eckert of ENIAC fame and others, is now constructing some new machines of a general purpose type.  This new digital computer is called the UNIVAC – Universal Automatic Computer – and is to be of a general purpose type suited for Bureau of Census work as well as, Army and Navy ballistics and fire control research.  The UNIVAC is to be very compact, using only about eight hundred tubes, and occupying only about as much space as five file cabinets.

It is rather interesting that one of the limitations of this and other digital machines is the slow rate at which numbers are printed at the output.  This limitation may be overcome in future machines by the use of a device called the “Numero-scope,” recently announced by the Harvard Computation Lab.  This device is nothing but a cathode-ray oscilloscope, which can trace the outline of any number, if the right signal is fed into its deflecting plates.  This is no mean trick – it takes six vacuum tubes to make the numeral 2, for example, but it has been done, and numbers may now be flashed on the screen of a cathode-ray tube and photographed with exposures as short as one five-hundredth of a second.

The analogue computer, as we have stated works with analogous quantities rather than with whole numbers.  Thus we may represent quantities by lengths, angles, voltages, velocities, forces and so on.  Thus an electrical or an hydraulic circuit problem may be solved on a mechanical device, while an electrical problem may be solved on a mechanical device.  One simple example of an analogue computer is the slide rule.  Here quantities of any sort are converted into lengths and since a logarithmic scale is used it is possible to multiply by adding lengths.  If a linear scale is used we can add by adding lengths.  Division and subtraction are possible by simply subtracting lengths in each case.

__________

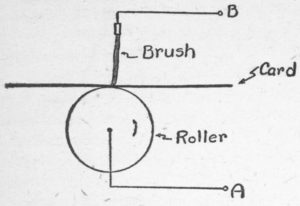
The basic mechanism in the punched-card machine is the brush and roller combination shown.  As the card passes over a steel roller, metallic brushes make an electrical connection – between A and B in the diagram – and a signal can be produced to reject the card, or set a counter wheel, et cetera.

__________

If we use angles, or angular displacements, to represent quantities successive displacements readily add to give a total.  We can also use a differential like the one in the rear end of a car to add the angular displacements in two different shafts.  The answer in this case, or a constant factor – gear ratio – times the answer appears on a third shaft.  Direct voltages add conveniently, and alternating voltages add like vector or directed quantities, and so are convenient in the solution of problems involving directed lengths or forces.

Before going any further into discussion of the specific details or these devices it might be well to examine the relative advantages and disadvantages of the analogue type of computer.  In the digital computer the accuracy can usually be increased at the expense of speed, so that if we want to go from 10 digit to 20 digit accuracy we must suffer a decrease to half the original speed.

With the analogue type of computer it is only possible to increase accuracy if the lengths – or angles, or voltages, or whatnot – are measured with greater percentage accuracy.  This may call for watchmaker techniques unless we can afford lengths or other analogous quantities.  The difficulties encountered in any case are such that the accuracy is always much less than in any digital machine.

There are several advantages possessed by the analogue computer which tend to offset the decreased accuracy.  One of these is its greater speed, which results partly from the fact that most problems are more easily set up for solution by analogue methods.  Sometimes the analogue computer is used for a quick look at a problem, to narrow down the field which must be investigated with greater accuracy by the more involved digital computer.  Another advantage possessed by the analogue computer is its ability – if the ability is built in – to perform certain mathematical operations in direct fashion.  Thus, for example, a pivoted rod can be used to give the sine of an angle.  This ability also accounts in part for the greater speed by the analogue method.  Still another advantage is ease with which empirical data in the form of curves may be fed into an analogue machine.

The first successful large-scale analogue computer was the Differential Analyzer designed by Dr. Vannevar Bush and others at M.I.T.  The same type of machine has also been built by General Electric for its own use and for use in various Universities.  The latest and most highly improved of these machines was recently installed at the new engineering school at U.C.L.A.

____________________

“1948-08-06: UCLA’s Differential Analyzer Begins Rise to Stardom“, at TomOwens YouTube channel.

Note that this YouTube clip shows the incorporation of the differential analyzer in the movies When Worlds Collide, from 2:00 to 4:13 (full length version here), and, Earth Versus the Flying Saucers, from 4:36 to end (in full-length version at Archive.org, from 59:28 to 107). 

____________________

The differential analyzer is used chiefly for the solution of differential equations.  In view of this fact it is rather strange that the machine cannot differentiate.  However it can integrate, and since this is the inverse of differentiation its mastery over the calculus is quite complete.  (The inverse of an arithmetical process is commonly used by clerks in stores who count back our change, and thus use addition in place of subtraction).  The integrators in a differential analyzer are of the Kelvin wheel-and-disk type in which an integrator wheel rides on a rotating disk, and is turned when the disk turns.  The amount of angular rotation of the integrator wheel depends on its distance, R, from the center of the disk, and the angle the disk turns through, θ.  This, by definition, is the integral of R with respect to θ. 

The integrator is the most important device in the differential analyzer, and as such has received a great deal of attention.  In 1944 G.E. engineers came up with a device in which troubles caused by slipping of the integrator wheel on the disk were virtually eliminated.  This device was essentially a servo follow-up system in which light beams were passed through a polaroid disk attached to a very light integrator wheel.  These light beams then went through other polaroid disks, then to phototubes, to an amplifier and a motor.  The motor then caused the second and third polaroid disks to follow the disk on the integrator wheel with the customary boost in power level, or torque level.

Among other important components in the differential analyzer are the input tables.  At these tables, in the older machines, operators followed plotted curves of functions which were to be fed into the machine with pointers, and thus converted distances on the curve sheets to angular rotations.  In the newer machines light beam photocell servo-mechanisms accomplish the same thing without the aid of skilled operators.  Known functions, of course, are generated by other and simpler means.

Because the differential analyzer handles quantities in the form of angular displacements the process of adding is accomplished by the use of differential gearing.  To solve a differential equation the machine must first be set up so that the right shafts are connected together by the right gear ratios.  When all is ready the data in the form of curves is fed into the machine at the input tables, the known functions are fed in from function generators, and the output pens are moved from left to right, all in synchronism.  Adding wheels, integrators, input table lead-screws and so forth all begin to move and perform the operations required by the equation being solved.  The totals of the quantities on each side of the equation are held equal by a servo-mechanism and the shaft which will give the function which is the desired answer moves the output pen up and down as it is pulled across a sheet of graph paper.  Thus the answer appears as a curve, or a set of curves.

The accuracy of these results depends not only upon the accuracy with which these final curves can be read, but also upon the accuracy of the original data, and the accuracy of the various servos involved in the solution.  Typically, about one-tenth of one percent, or three digit accuracy can be expected.  If some of the components have been forced to accelerate too rapidly because of a poor choice of gear ratio, or if a lead screw has been forced to the end of its travel, the solution may be completely wrong – the analyst still has his headaches.  These troubles are ordinarily avoided by making preliminary runs to determine the proper ranges of operation of all components.

Among the other types of analogue computers commonly used engineering work are the various kinds of network analyzers.  A large electrical power network may be exceedingly complex, due to the more or less random geographical distribution of loads and generating plants.  The effect of short circuits, arc-overs due to lightning, and load distribution must be studied with the aid of models, so that the design of circuit breakers, lightning arresters and so forth can proceed intelligently.  Tests cannot be made on the actual power network, as they can on communication networks, because of the possibility that damage to large and expensive equipment might result.

The earliest type of power network model was the D-C Network Analyzer.  The representation of three-phase alternating current systems by direct-current models of this kind has definite limitations, and the next step was the development of A-C Network Analyzers.  These models, although they represent a three-phase system by a single system are much more versatile than the D-C Analyzers.

We may ask if such models should really be classed as computers.  Fundamentally, these analyzers are merely models of systems which are too complicated for direct analysis, and too large for direct measurement of variables under all possible conditions.  Much the same kind of model-making is carried on in the study of aircraft antennas using model planes and microwaves in place of short waves.  However, if we examine some of the uses to which Network Analyzers have been put, it seems safe to class them as computers.  Because of the use of electrical quantities in these devices and because of the flexibility of interconnections possible, they have been used for the solution of such problems as the flow of microwave energy in wave-guides, the flow of compressible fluids in pipes, and even the solution of Schrodinger’s Wave Equation.

Another type of network analyzer is the Transient Network Analyzer, which can show more clearly what happens in a power network when short circuits and overloads occur.  This device may also be used to study analogous problems such as the amplitude of transient vibrations in mechanical systems when sudden shocks or overloads occur.  The inverse of this kind of thing is the mechanical model used to study what goes on in a vacuum tube.  In these models stretched sheets of dental rubber are used to represent electrostatic fields, and ball bearings serve as electrons.

The differential analyzer is more versatile than the network analyzer discussed above because it can integrate, differentiate – in effect – and multiply, and thus solve rather complicated differential equations.  These functions are performed by mechanical or electro-mechanical devices in the differential analyzer.  If these things could be accomplished by purely electrical means, we would expect a great increase in speed, and some decrease in size and weight.  Such machines have been built by Westinghouse and Caltech, and seem to promise a fair increase in speed over the old differential analyzer.  It seems inevitable that the use of many vacuum tubes will lead to somewhat lower accuracy and less dependability.  Another difficulty with present types of electronic differential analyzers is that integration can only be performed with respect to time as the independent variable, so that the solution of certain problems is not easily possible.

Many other kinds of analogue computers have been perfected in the last few years – the field is definitely “hot.”  Completed designs include such gadgets as the Bell Telephone M-4 Director, which used radar signals to figure out in a twinkling where an antiaircraft gun should be aimed so that the shell and a plane might meet.  Undoubtedly work is in progress on computers which will make possible solution the “problem of delivery” of the modern atomic warhead.  These latter-day buzz-bombs will be sufficiently lethal to warrant their carrying along their own computers.

Many scientists are disconcerted by the fact that by far the greater part of the computer research being carried on today is under the auspices of the Armed Forces.  To be sure, we in the United States seem to be far ahead of anyone else in the world in computers.  This may augur well for National Security if some desperate bludgeoning struggle is soon to occur.  From the longer range point of view it seems that it is particularly desirable that the scientist whose pure research may lead him to yet undiscovered fundamental truths be also equipped with this new and powerful tool.

__________

Three types of computers.  Top:  General Electric’s A.C. Network analyzer.  Middle:  The differential analyzer – of the analogue computer group – at General Electric.  Bottom:  The Bell Laboratories relay-operated digital computer.

References and Suggested Readings

Network Analyzer (AC power), at Wikipedia

Differential Analyzer, at Wikipedia

The UCLA Differential Analyzer: General Electric in 1947, Video at Computer History Museum

“The Differential Analyzer.  A New Machine for Solving Differential Equations”, by Vannevar Bush, at WorryDream

Differential Analyzer History, at LiquiSearch.com

A Brief History of Electrical Technology Part 3: The Computer, at Piero Scaruffi’s website

No Longer Missing: The Survival of Lt. JG William Robert Maxwell, United States Navy Fighter Squadron VF-11, May 2, 1943 – “A Castaway’s Diary”

“Just before sundown, rain began falling, the wind became stronger, and the waves got higher and higher.  There wasn’t much I could do – I was still weak and not a little scared.  About all I did was to throw out my sea anchor – a small rubber bracket on a 7-foot line – and cover myself with my sail.  Rain fell in torrents and the wind blew all night.  I bailed out water six or seven times during the night with the small cup that the pump fits in and also with my sponge rubber cushion, but there were always 2 or 3 inches of water in the bottom.  The rest of the time, I just huddled under my sail.”

________________________________________

The posts about the survival and return of Lieutenants Johnson and Landers pertaining to events in 1942, this post focuses on the experiences of Navy Lt. JG William Robert Maxwell in mid-1943.  A member of Navy Fighter Squadron VF-11, Maxwell was not shot down in aerial combat, per se, albeit he was forced to parachute during a combat mission.  This occurred on May 2, 1943, during his squadron’s first week of combat operations, when, while escorting a strike to Munda, his F4F Wildcat’s tail was sliced off by his wingman as the latter was switching fuel tanks.  Successfully parachuting from his fighter, Maxwell took to his life raft, in time successively reaching the islands of Vangunu, Tetepare (Tetepari) and Rendova, being rescued from the latter on May 17. 

While one commonality among the experiences of these three aviators is that they saved themselves by parachuting from their planes (rather than belly-landing or ditching their aircraft), another, more critical element, with I think greater relevance to survival and evasion – notably with Johnson and Maxwell – is that the very circumstances of their predicaments forced them to be self-reliant during much (Maxwell), or all (Johnson), of the time until their rescue.  (Landers didn’t have that problem, meeting native tribesmen very soon after landing!)  On the other hand, a central difference between the Army Air Force pilots and Maxwell is that a life raft was absolutely central to the latter’s survival – at sea.  Landing on land, neither Johnson nor Landers had no such problem.  (Well, Johnson had other problems!)          

Some time after his return, Maxwell wrote a detailed account of his experiences and survival, which was published in Intelligence Bulletin of December, 1943 (available at Archive.org).  As you can read below, where I’ve presented the article verbatim, Maxwell’s account has absolutely no identifying information (well, it was the middle of the war!) except for the calendar dates, and particularly, the first date – May 2 – when he was shot down.  Using this information, DuckDuckGo, and various websites (like Aviation Archeology) I was able to “pin down” the initially anonymous pilot’s name, identity his Squadron, and determine the Bureau Number of his F4F.  That led to Tillman and van der Lugt’s VF-11/111 ‘Sundowners’ 1942–95, which tied all the pieces together, the details matching the account in Intelligence Bulletin.  

Digressing…  Like many “things” one discovers while doing historical research, I found this article, and the journal itself, purely by chance: While researching a post covering a subject vastly different from WW II (albeit quite military in nature) … and then some!  Space Warfare, as described and conjectured in Astounding Science Fiction, in 1939. 

So, it would seem that researching fiction led to fact. 

__________

William Robert Maxwell later in WW II, probably while serving with VF-51.

__________

This is the relevant passage excerpt from Tillman and van der Lugt’s VF-11/111 ‘Sundowners’ 1942–95:

On 25 April 1943, after six weeks in the Fijian islands, CAG-11 departed for Guadalcanal.  White, Cady and Vogel each led one of VF-11’s three elements to their destination, with TBFs providing navigation lead on the 600-mile flight.  The Wildcats made the 4.5-hour flight to Espiritu Santo that day and logged another 4.3 the next, arriving at ‘The Canal’ on Monday the 26th with 34 aircraft.  Two had been delayed en route with mechanical problems, but both shortly rejoined the squadron.  ‘Fighting 11’ settled down at the Lunga Point strip better known as ‘Fighter One’, while Cdr Hamilton’s other three squadrons were based at nearby Henderson Field.  The ground echelon had previously arrived by ship or transport aeroplane and established a tent camp in what intelligence officer Lt Donald Meyer called ‘a delightful oasis of mud and mosquitoes in a coconut grove’. 

The next day VF-11 was briefed by Col Sam Moore, the colourful, swashbuckling Marine fighter commander.  The ‘Sundowners’ were to fly under the tactical control of the US Marine Corps, as the leathernecks had been operating from the island for the past eight months.  Later that morning (the 27th), VF-11’s first patrol from ‘Cactus’ was flown by Lt Cdr Vogel and Lt(jg)s Robert N Flath, William R Maxwell, and Cyrus G Cary.  It was a local flight with nothing to report, but two days later Lt Cdr White led two divisions on an escort to Munda.  The only enemy opposition was anti-aircraft (AA) fire.  Throughout the combat tour VF-11 was blessed with exceptional maintenance.  Prior to any losses, the unit maintained an average 37 of 41 available aircraft fully operational for an initial complement of 38 pilots.  The 90 percent readiness rate was partly due to the Wildcat’s relative simplicity, but it was also a tribute to Frank Quady’s maintenance crew.  The ‘Sundowners’’ mechanics certainly deserved their reputation, as they literally built an extra fighter from the ground up.  Using portions of three or four Marine wrecks, the sailors assembled another F4F-4 which they assigned the BuAer number 11!

At the end of the first week (Sunday, 2 May) VF-11 suffered its first loss.  Sixteen ‘Sundowners’ were escorting a strike to Munda when, south of Vangunu, at 14,000 ft the ‘exec’, Sully Vogel, ran one of his fuel tanks dry and lost altitude while switching tanks.  His element leader, Bob Maxwell, moved to port to regain sight of Vogel and the two Wildcats collided.  Vogel’s propeller sliced off the last six feet of Maxwell’s fuselage (BuNo 11757), the F4F nosing up in a half loop and then falling away in a flat spin.  Maxwell managed to bail out and opened his parachute, but the other Wildcats had to continue the mission.  At 1700 hrs the returning pilots spotted Maxwell in his life raft and reported his position, although it was too late to summon help.  Vogel had aborted the mission, returning with a smashed canopy and rubber marks on one wing from Maxwell’s tyres.  ‘Maxie’ was nowhere to be seen the next morning, and he remained missing for a full two weeks until a PBY Catalina brought him back to Guadalcanal on 18 May after a harrowing, but safe, 16 days in enemy-occupied territory.  The intrepid South Carolinian had sailed his raft to Tetipari, arriving on the 5th.  He walked the length of the island in seven days, encountering a crocodile that claimed dominion over a channel on a coral beach, but otherwise Maxwell met no opposition.  On the 13th he launched his raft for Rendova, where he knew he might contact an Australian coast watcher.  He was met by friendly natives who took him to safety near Segi Lagoon on the 17th. 

__________

This Oogle Map shows the Solomon Islands.  Vangunu, Tetepare (Tetipari), and Rendova are situated in the “center”, as it were, of the archipelago.  

__________

Here’s a closer Oogle Map view of Vangunu, Tetepare (Tetipari), and Rendova. 

 

__________

Finally, an air photo / satellite view of the same three islands.  (This image is from Duck Duck Go, not Oogle.)    

__________

Also from Tillman and van der Lugt’s VF-11/111 ‘Sundowners’ 1942–95:

Maxwell’s fifth mission had been his last with VF-11, for he was flown to New Zealand, where he spent the next spent two months in hospital, recuperating from his adventure.  Subsequently he joined VF-51, becoming the squadron’s only ace aboard USS San Jacinto (CVL-30) in 1944.

__________

The original source of Maxwell’s report:  Intelligence Bulletin for December, 1943, from Archive.org.

__________

And so, here’s Robert Maxwell’s report…

Section III.  A CASTAWAY’S DIARY

1. INTRODUCTION

A U.S. aviator, forced to parachute from his plane in the South Pacific, spent two trying weeks on the sea and on practically uninhabited islands before he was rescued.  He kept a day-by-day account of his experiences, relating how he utilized his equipment, the mistakes he made, and how he obtained food and water.

A condensed version of this pilot’s diary is presented below.  In addition to being interesting, his story is believed to contain lessons which will be profitable for other members of our armed forces.  It is considered that the safe return of this pilot to his squadron should be attributed to his resourcefulness and the intelligent use he made of his equipment.  The fact that he knew where he was and where he wanted to go, and knew how to go about getting there saved him from a great deal of futile wandering and mental distress.

The names of persons and places have been omitted from the story.

2. THE DIARY

May 2 [1943]

The opening of the ‘chute snapped me up short, and I was able to look around and see my plane falling in two pieces – the tail section and about 6 feet of fuselage were drifting crazily downward and the forepart was fluttering down like a leaf.  I tried to ease the pressure of the leg straps on my thighs by pulling myself up to sit on the straps, but was unable to do so because of the weight and bulk of my life raft and cushions.  As a result, my thighs were considerably chafed.

I was so busy looking around that I didn’t notice how fast I was descending, and before I knew it I had hit the water.  The wind billowed the ‘chute out as I went under, and I was able to unfasten my chest strap and left leg strap at once; unfastening the right strap took about 45 seconds, and I held on to the straps as I was pulled along under water by the ‘chute.  I couldn’t understand why I didn’t come to the surface – then I remembered that I hadn’t pulled the CO2 (carbon dioxide) strings of my life jacket.  As soon as I had done this, my belt inflated and I came to the surface.  I immediately slipped my life raft off the leg straps, ripped off the cover, and inflated it.

During my descent I had hooked an arm through my back pack strap so as not to lose it, but during the time I was struggling under water it must have come off because, when I came up, I saw it floating about 20 feet away.  I paddled over and picked it up, along with two cushions – one of which was merely a piece of sponge rubber, 15 inches square and 2 inches thick.

After I got into the boat, I took the mirror from the back pack and discovered a deep gash, about 14 inches long, on my chin and another deep gash, about 3 inches long, on my right shin.  I took out my first-aid kit, examined the contents, and read the instructions.  I found that there was no adhesive tape in the kit – apparently it had not been replaced when the kit was checked on the ship coming down from Pearl Harbor.  I sprinkled sulfanilamide powder on both wounds and put one of the two compress bandages on my leg.  I haven’t any idea how I got either one of these cuts.  During this time I was having brief spells of nausea, but did not vomit.  However, in a short while I had a sudden bowel movement, probably as a reaction from the shock and excitement.  I felt very weak and dizzy.

I began to take stock of my equipment and to figure out where I was by consulting the strip map which I had in my pocket.  My chief aim was to reach the nearest land.

As I sat in the boat, still dazed and faint, I realized that, with the distance and prevailing northeast wind, I had little chance of making one of the larger islands.  As nearly as I could figure out, I was about 10 miles east of a small island and about 10 or 15 miles south of another.  Beyond reaching land I hadn’t formulated any plans except to reach land.

About 50 minutes after I had crashed, I saw a friendly fighter coming toward me from the west, about 50 feet off the water.  I immediately grabbed my mirror and tried to flash the plane.  The pilot wobbled the plane’s wings, came in, and circled, and I saw that it was my wing man.  Five other fighters came down and circled, apparently trying to get a fix on me, and I waved to them.

Soon they went off toward the cast, and I noticed to my consternation that dark cumulus thunderhead clouds were moving in quickly from the northeast and that the sea was getting quite rough.  I realized that no planes would come out for me then because of the approaching dusk.  Just before sundown, rain began falling, the wind became stronger, and the waves got higher and higher.  There wasn’t much I could do – I was still weak and not a little scared.  About all I did was to throw out my sea anchor – a small rubber bracket on a 7-foot line – and cover myself with my sail.  Rain fell in torrents and the wind blew all night.  I bailed out water six or seven times during the night with the small cup that the pump fits in and also with my sponge rubber cushion, but there were always 2 or 3 inches of water in the bottom.  The rest of the time, I just huddled under my sail.

May 3

The rain stopped about daybreak, but the sky was cloudy and the sea still choppy.  Off to the east I saw what appeared to be two friendly fighters in the distance, but I knew they wouldn’t see me.  As day approached, I saw that I had been blown about 10 miles south of the center of the island I was making for.  The, wind was still from the northeast and I knew I would have to paddle like the devil even to hold my own and not be blown farther out to sea.  I broke out one of my six chocolate bars and ate part of it, but I wasn’t hungry.  I also took a swallow out of my canteen, but I wasn’t particularly thirsty.  All day long I rowed with my hand paddles, sitting backward in the raft.  By 1600 my forearms were raw and chafed from rubbing against the sides of the raft.  I had stopped paddling only two or three times during the day, to eat a bite of chocolate and take a swallow of water.  Rain began falling about 1600, and I hit a new low point of discouragement when I realized that I had apparently made no headway at all during the day.

After night fell, the rain continued in intermittent showers until dawn.  The sea was still rough and the wind was from the northeast.  I tried to continue paddling, but a large fish hit my hand – I don’t know what kind it was – in fact, I didn’t even see it, but the experience dissuaded me from rowing any more in the dark.  I threw out my sea anchor again – this time with the two cushions tied on the line for additional weight – and huddled under my sail for the rest of the night.  I don’t recall that I slept this night, or any night before I got to shore – I just seemed to lie in a sort of coma.

May 4

When the sun came up, I found that I was south of the west end of the island and about two miles farther out than I had been the previous morning.  I broke out another chocolate bar for “breakfast,” drank a little water, and began to paddle again.  Some time during the day I got the idea of getting in the water and swimming along with the raft.  The only result of this maneuver was that I lost one of my hand paddles, and I went back to paddling with the remaining paddle and my bare hand.

The results of my continuous paddling were more heartening this day, and by about 1500 I realized that I had covered quite a little distance.  Just about this time, however, a big storm came from the northwest, and it began to rain again.  Again I put out my sea anchor with the cushions tied to it, and settled down under my sail.  It rained off and on all night with a northwest wind.  Although I was never very thirsty, I would catch rain on my sail and funnel it into the pump cup, drink some of it, and use the rest to keep my canteen filled.  Before the storm came that afternoon, the sun had been quite hot and I had kept my head covered with my sail and applied zinc oxide to my face.  Earlier that day I had seen four friendly fighters, going west along the south shore of this island.  I also saw a friendly patrol plane which passed over early every morning and late every evening, but because the sun was so far down each time, I was never able to signal with my mirror.

May 5

At daybreak I saw that I had drifted to a point about 6 miles south of the east end of the island.  I had another chocolate bar for breakfast and a little water, and I was considerably encouraged when I found that the wind was blowing from the southeast.  This meant that I had a very good chance of reaching the island, so I pulled in my sea anchor and began paddling.  Some time during the morning my remaining hand paddle slipped off in the water and, forgetting that I had my life belt inflated, I jumped overboard to retrieve it.  Of course, I couldn’t get under the surface and soon gave up.

I stopped paddling only to take an occasional swallow of water, and about 1800 I came close to the shore.  The surf didn’t look too bad.  I headed right in – a mistake, as it turned out, for as soon as I got in closer I found that the waves were at least 50 feet high (*), the highest surf I’ve ever seen.  About this time a big one broke.in front of me.  It was too late to turn back.  I felt as if I were 50 feet in the air when it broke, and all I could see in front of me was the jagged coral of the beach.  I tried to beat the next one in, but it caught me just after it broke and tossed me end-over-the-kettle into the coral.

Fortunately, I missed hitting the sharpest coral and received only a few cuts on my hands.  My boat landed about 50 feet away in a sort of channel leading into the beach.  I tried to stand up and found that I couldn’t walk.  Finally, I crawled over to the little channel, got my boat, and dragged it up on a small sandy beach.  Since I had tied my belongings rather securely to the raft, the only items that were missing were the pump, the two cushions, and the can of sea marker.  I was very tired and very weak; I turned my raft upside down and lay on it, with my sail over me, trying to sleep, but apparently I was too tired to sleep – I think I only dozed for periods of a few minutes at the most.

May 6

At dawn I began to look for coconuts on the ground and found one mature nut under a tree.  The tree was about 25 feet high, and I immediately set to thinking how I could get more of the nuts off it.  I was, of course, too weak to climb and I thought of cutting notches in the tree.  It was hopeless, and I opened the one coconut.  The seed had already sprouted and there wasn’t much milk in it; since I wasn’t hungry, I ate only a little of the meat.

Instead, I had my usual “breakfast” of a chocolate bar, laid out my things to dry, cleaned my knife and gun as best I could, and rested some more.  Although my .45 had been wet almost constantly and was quite rusty, the moving parts worked all right after I had applied more oil to them.

Then I started out to find some pandanus nuts, having read and reread my guidebook.  I found a few, but they were so high I couldn’t get to them.  In the afternoon I sorted my equipment and rested.  By this time I had decided to try reaching the western end of the island.  I wasn’t sure whether there were any Japs or natives on the island, but thought I might at least run into some natives.

During the day I ran across a crocodile in a channel in the coral beach, but we parted company at once, without incident.  Toward evening, rain threatened.  I made a coconut cup, imbedded it in the sand, and rigged my sail around it so that it would catch water and funnel it into the cup through a small hole in the sail.  The rain began when it got dark.  I settled myself on the ground under a tree and pulled my rubber boat over me for shelter.

May 7

In the morning I worked out a plan for getting some coconuts.  I cut several notches in the trunk of the tree and then made a sort of rope ladder with my sea anchor line, placed this around the trunk so that it would slip, and pushed it up as far as I could.  Climbing up by these means, I was able to reach and twist off two coconuts.  This was pretty exhausting work, so I rested for a while and then filled my canteen with the rain water that had accumulated in the coconut cup.  I drank the milk from the coconut and ate a little of the soft meat, but still I was not very hungry.  My store of chocolate bars was down to two, so I decided to conserve them.

I then packed all my gear in my back pack, rolled up my life raft, and set out to walk along the coast to the west end of the island.  There was a 100-yard stretch of coral between the water and the beach, and it was not bad walking.  Naturally, I was glad I hadn’t discarded by shoes in the water.  Several times I came to channels in the coral, usually at the mouths of small streams, and then I would have to blow up my life belt and swim across.  At one such “place I saw more fish and tried to catch one with my fishing line and pork-rind bait, but the fish declined to bite.

Late in the day I came to a sandy beach, along which I walked until it was dark.  Then I made a crude lean-to of palm fronds against a tree trunk, blew up my life raft, and settled down on it with my sail as a cover.  I smeared zinc oxide on my face – I put either zinc oxide or vaseline on my face each morning and night for protection against sunburn, and also periodically put vaseline on the gash on my shin and on my hands, which were cracked from the salt water.  The sulfanilamide powder was rather water-soaked, so I used vaseline instead.  Aside from a daily quinine pill, that was the extent of my doctoring.  Fortunately, the gash on my chin had closed pretty well.

That night I woke up from one of my periods of dozing to find that the tide had come in.  I scrambled around, moving my gear to a dry spot, and discovered that the tide had carried away my sail and my shoulder holster.  Luckily, I had my .45 close to my side, but one of the two clips in the holster contained all my tracer bullets.

May 8

In the morning, after I had eaten half of my remaining chocolate bar, I started walking again.  Most of the time I walked in the water up to my knees.  Soon the coral ledge ended and I had to strike inland because I couldn’t get through the immense surf that was washing against the high rock and coral of the shore.  I would go inland a little way, parallel the coast by clambering up and down the ridges, and then go back to the shore to see if I could make my way along it.  During the day I saw two more crocodiles in a small lagoon and my only snake, a small blue snake about 1 1/2 feet long with a flat tail.  During the day I found several coconuts along the beach and on the ground, and I drank the milk.  As dusk came on, I was inland, climbing one of the ridges.  It began to rain.  I put my life jacket and back pack on the ground, under a log, and lay on my deflated life raft.  It rained all night, and by morning I was lying in mud.

May 9

During the morning I crossed more ridges, which ran down to the shore from the central range.  This was pretty tiring – mostly I would zigzag up them, and then slip and slide down.  I was always hopeful that I would be able to make my way along the coast, but this was impossible.  During the day I ate some fern leaves and the remainder of my last chocolate bar.  At dusk I came down to the coast to see whether I had rounded a particular rocky point.  I found that I hadn’t, and decided to spend the night in a small cave in the coral, which was about 100 feet above and 150 feet back from the water.  I slept on my back pack and life jacket and used my deflated raft as a cover.  After sleeping spasmodically, I was awakened at dawn by a wave breaking at the entrance to the cave.

May 10

In the morning, rain was falling and the wind was blowing; I could make little headway over the rocks and coral so I took to the ridges again.  I ate some ferns, and about 1450 I came onto the shore where there was a good sandy beach.  The hills were smaller, and there was a grove of coconut palms.  I was near the end of the island and could see the next one about 2 or 3 miles across the channel.  In the shallow water I found two small crabs and about eight mussels.  I ate the crabs raw, and, putting the mussels in my pocket, headed for a small bay.  It was a fine afternoon and I built a lean-to of sticks and palm fronds and blew up my raft.  I then tried some of the mussels and found that they were rather unpleasantly slimy.  When I ate the rest the next day, I washed them first and they tasted pretty good.   It rained that night, and since my lean-to did not prove to be as water-proof as I had expected, I got under my boat.

May 11

The next morning I rested, and ate the meat and drank the milk of a few coconuts.  I decided not to build a fire because of the possibility of attracting Japs, but to get to the next island and try to make contact with the natives.  I filled my canteen from a stream.  Late in the afternoon a number of friendly bombers and fighters came over going west and soon returned.  Both times I used my mirror to try to attract their attention.  I was quite weak and tired, but built a new and better lean-to.  That night I dozed fitfully and the mosquitoes were quite annoying.  The only other noteworthy incident that day was my first bowel movement since the one immediately after parachuting into the sea.

May 12

In the morning I washed my clothes and set about making some oars.  I found two small pieces of lumber with a few nails and a screw in them, and, using the nails and a screw, I attached two sticks to the pieces of lumber to make a serviceable pair of oars.  Then I ran my sea anchor line around my boat through the rings, and attached to it another piece of rope that I had found.  I made two loops in the rope for oar locks.  By looping the rope around my feet I could get leverage for rowing.  I used some sponge rubber from my back pack to make pads for oars.  I slit my back pack and inserted a couple of sticks; this provided me with a sail.  When I had completed my preparations in the evening, I gave my craft a brief shake-down cruise, dined on coconuts, and went to sleep.1

May 13

With the meat of two coconuts and my canteen of water as provisions, I set out early in the morning on my voyage to the next island.  I went out to sea through a break in the reef and soon found that, although my course was due west, I was heading northwest.  This was due to a north-northeast wind, and I rowed constantly because of the possibility of being blown south Of the hook of the island.  About noon I headed into a sandy beach on the south shore of the hook and again found to my dismay that I had underestimated the size of the surf.  The waves caught me and tossed me onto a fairly smooth coral ledge.  I was under water for what seemed a very long time – actually about 45 seconds – but managed to hold onto my boat.  As I struggled to my feet I heard someone shouting and was overjoyed to see two natives in a canoe about 50 yards off shore waving to me.

I got into the canoe with all my gear except the back-pack cover and we started east to the south shore of the point, where we met two more natives in another canoe and put into the beach.  The natives brought some water and a taro from a hut.  After a while we started around the point and along the shore.  The natives asked me if I were thirsty, and when I said that I was, we again put into the beach and went into another hut, where I saw a collapsible Japanese boat.  One of the natives climbed a 50-foot coconut palm and brought me some coconuts.

Finally we pushed on to a village about halfway up the coast.  There I was greeted by the chief.  After being given pineapple and taro, I was taken to another hut where it was indicated that I was to sleep.  I was given a corner of a low platform, a clean bamboo mat, and a pillow and blanket.  After eating more pineapple and taro, I talked mostly with the chief’s son, who had been to a mission school and was quite interested in America.  After dark we all went to sleep.

Traveling from island to island for three days, the natives managed to get me to the U.S. outpost, where I was picked up and carried back to my organization.

(*) This height, estimated by the writer, is believed to be excessive.

References

Intelligence Bulletin, V II N 4, December, 1943, Military Intelligence Division, War Department, Washington, D.C.

Tillman, Barret; van der Lugt, Henk; Holmes, Tony, VF-11/111 ‘Sundowners’ 1942–95 – Aviation Elite Units 36, Osprey Publishing Company, London, England, 2012


Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/emc2ftl3/public_html/wp-includes/formatting.php on line 4365