Astounding Science Fiction – History, at Random

Before The Web: Computation and Cybernetics in Astounding Science Fiction, May, 1949 – “Electrical Mathematicians”

From Astounding Science Fiction of May, 1949, the article “Electrical Mathematicians,” by Lorne Maclaughlan, focuses on the the use of computers – specifically, electronic as opposed to purely mechanical computers – as devices to perform mathematical calculations. It’s one of the four non-fiction articles pertaining to cybernetics and computation published by the magazine that year, the other three having been:

“Modern Calculators” (digital and analog calculation), by E.L. Locke; pp. 87-106 – January

“The Little Blue Cells” (‘Selectron’ data storage tube), by J.J. Coupling; pp. 85-99 – February

“Cybernetics” (review of Norbert Wiener’s book by the same title), by E.L. Locke; pp. 78-87 – September

The identity and background of author Maclaughlan remain an enigma. (At least, in terms of “this” post!) The Internet Speculative Fiction Database shows only two other entries under his name, both in Astounding (“Noise from Outside” in 1947, and “Servomechanisms” in 1948, while web searches yield a parallel paucity of results. This absence biographical information, especially in light of the over seven decades that have transpired since 1949, coupled with the author’s distinctive writing style – combining clarity and economy of expression, and, an ease and familiarity with the language of technology – leads me to wonder if that very name “Lorne Maclaughlin” (note the lack of a middle initial?) might actually have been a pen-name for an engineer or academic. Given the somewhat ambiguous reputation of science-fiction in professional and credentialed circles (albeit a reputation by the 1940s steadily changing for the better) maybe “Maclaughlan” – assuming the name was a pseudonym – might have wanted to maintain a degree of anonymity.

Well, if so (maybe so?!) that anonymity has successfully persisted to this day!

Anyway, the cover art’s cool.

Depicting a scene from the opening of Hal Clement’s serialized novel Needle (the inspiration for the 1987 Kyle MacLachlan film The Hidden?), it’s one of the three (color, naturally) Astounding Science Fiction cover illustrations by Paul Orban, an illustrator primarily known for interior work, whose abundant output was only exceeded by his talent.

As for Maclaughlan’s article itself, it begins with a brief overview of the implications of the increasing centrality of calculating devices in contemporary (1949 contemporary, that is!) society, and the future.

This is followed by a discussion of the very nature of calculation, whether performed by mechanical or electronic devices, which then segues into a comparison of the similarities and differences between binary and decimal systems of counting and computation, and an explanation of the utility of the former in computing devices.

Next, a lengthy discussion of memory. (We’ve all heard of that…) note the statement, “Not only must we “teach” the machine the multiplication table – by the process of wiring in the right connections – but it may also be necessary to provide built-in tables of sine and cosine functions, as well as other commonly used functions. This is a permanent kind of memory – a fast temporary kind of memory is also needed to remember such things as the product referred to above until it is no longer needed. This memory has not been easy to provide in required amounts, but recently invented electronic devices seem to offer some hope that this difficulty can be overcome.” In this, author Maclaughlan is anticipating what we know today as ROM (read-only-memory) and RAM (random-access-memory), respectively. This is followed by the topic of data input and manipulation, in the context of Hollerith Cards and Charles Babbage’s “Difference Engine”. (For the latter, see “Babbage’s First Difference Engine – How it was intended to work,” and, “The Babbage Engine,” the latter at Computer History Museum.

From this, we come to computation in terms of the technology and operation of then-existing computers. This encompasses ENIAC (Electronic Numerical Integrator and Computer), EDVAC (Electronic Discrete Variable Automatic Computer), and MANIAC (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I), and briefly touches upon the Selectron tube, the latter device the subject of J.J. Coupling’s article in the February 1949 issue of Astounding.

The final part of Mclaughlan’s article is a discussion of the nature, advantages, and use of “analyzers” – Differential Analyzers, and Transient Network Analyzers – in computation: Specifically, in the solution of differential equations pertinent to scientific research, such as, “…the flow of microwave energy in wave-guides, the flow of compressible fluids in pipes, and even the solution of Schrodinger’s Wave Equation,” or military applications, such as aiming anti-aircraft guns or determining the trajectory of nuclear weapons, noting, “These latter-day buzz-bombs will be sufficiently lethal to warrant their carrying along their own computers.”

Prescience, or, inevitability?

And finally, the article concludes with a photograph.

And, so…

ELECTRICAL MATHEMATICIANS

“The differential analyzer is more versatile than the network analyzer discussed above because it can integrate, differentiate – in effect – and multiply, and thus solve rather complicated differential equations. These functions are performed by mechanical or electro-mechanical devices in the differential analyzer. If these things could be accomplished by purely electrical means, we would expect a great increase in speed, and some decrease in size and weight.”

To an extent none of us today can realize, these rapidly growing electrical calculators will become more and more important factors in ordinary life. So far, they are handling only simple, straight-arithmetic problems. They are brains, but so far they think only on low levels. Give them time; they will be planners yet!

In this machine age no one is surprised at the announcement of some new or improved labor-saving device. The scientists and technologists who design our new electronic rattraps, microwave hot-dog dispensers and atomic power plants have succeeded so well that they have created a serious manpower shortage in their own professions. This shortage, which is chiefly in the field of analysis has recently forced them to put an unprecedented amount of effort into the design of machines to save themselves mental labor. The results of their efforts are an amazingly variegated collection of computing machines, or “artificial brains” as they are called in the popular press:

The development of such machines took a tremendous spurt during the war, and today we can scarcely find a laboratory or university in the land which is not devoting some part of its efforts to work of this kind. Progress is so rapid that the machines are obsolete before they are completed, and thus no two identical machines exist.

We cannot say that the computing machine is a new invention – the unknown Chinese originator of the abacus provided man with his first calculating machine in the sixth century B.C. This would seem to make the machine nearly as old as the art of calculating, but man is equipped with fingers and toes which have always provided a handy portable computing device. In fact, as we shall see, the simple fact that we have ten lingers has a definite bearing on the number of tubes and the kind of circuits required in electronic digital computers.

__________

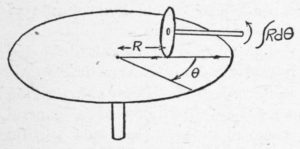
Kelvin Wheel-and-Disk integrator. This device, which gives the integral of a radial distance with respect to an angle, is the most important unit in a differential analyzer of the electromechanical type.

__________

It should be pointed out that there are two distinct types of computing machines in common use today. One type deals with discrete whole numbers, counting them off with the aid of teeth on a wheel, or electrical pulses in vacuum tube circuits. These numbers represent quantities, and they are added and multiplied just as numbers are on paper, but at a much higher speed. These machines called digital computers, range from the simple cash-register adding machine to the complex all-electric ENIAC, with its eighteen thousand radio-type vacuum tubes.

The other type of machine is the analogue type of computer, in which the number to be dealt with is converted into some measurable quantity, such as length along a slide rule, or angle of rotation of a shaft. The operations are performed electrically or mechanically, and the answer appears as a length, an angle, a voltage or some other quantity which must be converted back to a number. The ideal machine of the analogue type will accept mathematical functions, empirical curves and directions for mixing and stirring, and turn out results in the form of curves automatically.

The digital computer is much more accurate than the analogue type for the simple reason that is easy to extend the number of significant digits in such machines to something like thirty or forty. It is impossible to measure a point on a curve to anything approaching one part in 1040. However, the analogue computers are in many ways faster and more versatile, because they can perform certain difficult mathematical operations directly, while digital machines require that these operations be reduced to addition and multiplication.

One of the first things we must do to understand modern digital computing machines is to disconnect our minds from the decimal number system, and get a more basic concept of number representation. The decimal system of numbers is a natural choice, based on the fact man has that ten fingers. We would perhaps be more fortunate had evolution given us twelve, for then our number system would be the more convenient duo-decimal system. Let us examine this system as a starting point, by studying the table of numbers below.

1	2	3	4	5	6	7	8	9	*	t	10
11	12	13	14	15	16	17	18	19	1*	t	20
21	22	23	24	25	26	27	28	29	2*	t	30

The six-fingered man would count to six on one hand, and then continue, seven, eight, nine, star, dagger, ten on the other. His ten would be our twelve, of course, but it would be a resting point for him while he got his shoes off to continue to his twenty – our twenty-four – on his twelve toes.

If we continue the table for twelve lines of twelve numbers each we will get to his one hundred, which corresponds to our one hundred forty-four. This number is his ten squared – our twelve squared – as it would be, and is preceded by his daggerty-dagger, ††. This duodecimal system has the advantage that ten can be divided by 2, 3, 4 and 6, giving in each case whole numbers – 10/4 = 3, 10/6 = 2, et cetera – while our ten is only divisible by 2 and 5. The ancient Babylonians were fond of this system, and also used sixty as a number base. These systems remain today as the bases of our measurement of time in seconds, minutes and hours.

Now let us examine the binary system, based on two. In this system all numbers are made up of combinations of just two digits, one and zero. The simplicity of this system makes it possible to use simple devices such as electromagnetic relays to represent numbers. The simple relay has two possible positions, open and closed, and we can represent zero by means of the open position, and one by the closed position, and then build up any number as shown in the table below.

Decimal System	Binary System
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010

Computation is easy with this system, once we get the hang of it. Thus our two cubed becomes, 1011 = 10 x 10 x 10 = 1000, and our two times three becomes 10 x 11 = 110, which is our six, as it should be.

With our minds cleared for action on any number base let us consider the capabilities which are necessary in a digital computer. Digital computation requires that all operations be reduced to those of addition, subtraction, multiplication and division whether a machine is used or not. These operations involve certain reflex actions, such as the response “six” when presented with the numbers “two” and “three” and the idea “multiply.” The trained human mind possesses such reflex actions, and the machine must also possess them, as a first requirement. Simple computing devices such as the commercial accounting machine possess a few reflexes. It is necessary to build many rapid reflexes into mathematical computing machines.

The next “mental” capability the machine must possess is that of memory. When we must multiply two numbers together before adding them to a third, memory is needed to preserve the product until the second operation can be performed. Commercial calculating machines have limited memory – after multiplication, for example, the number appears on the output wheels, and the third number can easily be added. The memory requirements in a good mathematical machine are much, much more stringent, and provide some of the toughest problems in design. Not only must we “teach” the machine the multiplication table – by the process of wiring in the right connections – but it may also be necessary to provide built-in tables of sine and cosine functions, as well as other commonly used functions. This is a permanent kind of memory – a fast temporary kind of memory is also needed to remember such things as the product referred to above until it is no longer needed. This memory has not been easy to provide in required amounts, but recently invented electronic devices seem to offer some hope that this difficulty can be overcome.

There are still two capabilities left. These are choice and sequence. The computing machine should be able to choose between two numbers, or two operations it can perform, in accordance with certain rules. Sequence involves, as the name implies, the proper choice of order of numbers or operations according to some rule which applies in the particular problem being solved.

These last two capabilities are not found to any great extent in any but the most modern mathematical computing machines. On the other hand there are a multitude of other mental capabilities found in humans which are undesirable in mathematical machines. Emotion, aesthetics, creative ability and so forth are not desirable, for these help to make humans unfit for much routine computing work. What we want is perfect slave, fast, untiring and industrious, who will never embarrass or disconcert us with unexpected response. (Of course the engineers in charge of some of the complicated modern mathematical machines are quick to accuse them of temper tantrums and other undesirable emotions.)

Perhaps the fanciest digital computing machine today is the IBM Automatic Sequence Controlled calculator at Harvard. The letters IBM International Business Machines Corporation, which has developed a series of machines intended for use in accounting work. These machines use a punched card – a device with quite a history, as histories go in the computing field. It would seem that weaving machines which could be used to more or less automatically weave patterned cloth excited the imagination of a good many inventors in in the early eighteenth century. In such weaving it was necessary to sequence automatically the “shredding,” or controlling of the warp threads so that weft threads could be passed through them to weave a pattern. Punched tape and punched cards had already been by 1727. The punched cards we use today get the name Jacquard cards from the name of the inventor of an improved weaving machine around the year 1800.

This basic idea was good enough to attract the attention of Charles Babbage, an English actuary, who is regarded as the lather of the modern computing machine. His “difference engine” was designed, in his words, “to perform the whole operation” – of the computing and printing of tables of functions – “with no mental attention when numbers have once been fed in the machine.” When this “engine” was nearly complete the government withdrew its support of the Project, and Babbage began the construction of an analytical machine on his own. This machine, a wholly mechanical device, was to use punched Jacquard cards for automatic sequencing. In 1906 his son successfully completed a machine with which he calculated pi to twenty-nine significant figures.

Hollerith, in this country, made a great advance in the use of punched cards when he invented a card sorter to aid in classifying the results of the 1880 census. Most people today are familiar with the kind of things that a sorter can do. Thus if we have a sorter and a stack of cards with personal and alphabetical information punched thereon we can request the machine to pick out all left-handed individuals with cross-eyes and Z for a second initial, and bzzzzt, bzzzzt, bzzzzt – there they are.

The IBM Company, by catering to the needs of organizations which handle – and have – a good deal of money, was able to put the manufacture of computing machines on a paying basis. It need not be pointed out that it is much more difficult to produce profitably machines which will only be used for such tasks as the calculation of pi to umpteen places. However the punched card machines built for accountants have found their way into scientific computing laboratories, and the IBM Company has a research laboratory which is actively developing new machines for scientific use as well as for accounting.

A punched card machine operating on the Hollerith principle interprets numerical and operational data according to the positions of holes punched on cards, and then perform various mathematical operations. The cards, which are familiar to most people – postal notes, government checks, et cetera – have twelve vertical positions in each of eighty columns. The vertical positions are labeled y, x, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Thus an 80 digit or two 40 digit numbers can be set up on one card, and the y space, for example, may be used to indicate sign.

The cards are read for purposes of sorting et cetera by a simple mechanism involving a metal cylinder and sets of electrically conducting brushes. As the card moves between the rotating cylinder and the eighty brushes, one for each column, an electrical contact is made whenever a punched hole passes under a brush. The position of the cylinder at the time that the brush makes contact indicates the number, or letter, represented. Any number system could be used, but the decimal system is selected because of its familiarity. The various IBM machines now on the market include Card Punchers, Card Interpretaters [sic], Card Sorters, Collators and others, all operating on the same basic principles. The most useful machine to scientific workers is the Automatic Multiplying Punch. This machine will multiply factors punched in cards, and will automatically punch the product in a card, or even add and punch out products.

The computer lab at Harvard, mentioned above, uses a combination of these machines and a device for sequencing their operations – whence the name IBM Automatic Sequence Controlled. This calculator is one of the half-dozen large machines in this country which can be used to tear into a tough problem and quickly reduce it to a neat column of figures – or a stack of cards, in this case. Since it is a digital type of computer capable of great accuracy, but because it is partly mechanical in operation it is slow compared to the newer all electronic machines. The automatic sequencing apparatus is not easy to set up, and thus type of machine is best suited to the solution of repetitive types of problems, such as the calculation of tables. The punched card is a convenient form in which to store tables of simple functions, e.g. Sin x, Log x, which are often needed in computation of tables of more complicated functions.

Of course, if you want to prepare a table umpteen places Bessell Functions, or evaluate some determinants, or make some matrix algebra manipulations you will have to wait s time for your turn on this or any similar machine. You will have to have a pretty good story too, for these machines are at work today, and sometimes night as well with important problems. It must be realized too, that a problem be rather important and complex before it is even worthwhile to the labor of setting it up for solution in such a complicated machine.

Punched cards are often used to store scientific data other than tables with the advantages of machine sorting et cetera possible with IBM machines. Thus at the Caltech wind tunnel data from instruments is punched directly on cards. Astronomers locate star images by pre-computed co-ordinates on punched cards, and then measure the star positions accurately and record the new information on new cards. The Census Bureau makes a great deal of use of punched cards at present, but plans are being made to go over to the faster electronic computers for this work.

__________

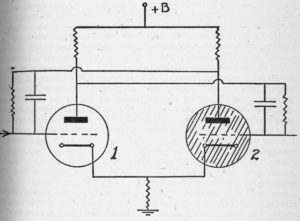
Basic flip-flop vacuum-tube circuit used in the ENIAC and in other digital computers. Tube number 2 – shaded – is conducting, and tube number 1 is “cut-off”, in the diagram above. A positive pulse on tube 1 will cause it to conduct and the resultant drop in its plate voltage will cause tube 2 to cease conducting. This condition is stable until another pulse arrives, on the grid of tube 2.

__________

Shortly before the war, G.R. Stibitz and others at the Bell Telephone Laboratories developed a relay type of computer which could handle not only real numbers but complex numbers as well. The binary number system is convenient in a relay computer as we have pointed out. There is some difficulty entailed in the process of getting from a number expressed in the ordinary decimal system to the binary system and back again. For this reason Stibitz likes what he calls a bi-quinary system, which uses base 2 to tell if a number is between 0 and 4, or 5 and 9, and base 5 to tell which digit it is of the five. Early in the war the Army and Navy each ordered one of these relay computers, and machine computation was off to a flying start.

Dr. H.H. Aiken, who had built the IBM computer at Harvard has recently gone over to the relay type of computer, and his “Mark II” will soon be in operation on the complicated guided missile ballistics problems being studied at the Dahlgren Proving Ground. IBM has also been playing around with relay computers, and has delivered two sequence controlled machines of this type for ballistic research workers. Aiken does his sequencing with standard teletype tape, while some of the IBM jobs use plugboards.

An interesting example of a similar parallel development is the Zuse computer, named after its designer Conrad Zuse, who developed his machine in Germany during and since the war. Like the Bell Laboratories machine it uses a keyboard to feed numbers into its relays. The sequence is prepared in advance by an operator who punches instructions into a strip of film.

The art of machine computation took a tremendous jump ahead when in the fall of 1946 the ENIAC, the first electronic digital machine, was placed in operation. This machine was built for Army Ordnance at the Moore School of Engineering by J.W. Mauchly, J.P. Eckert and others. The ENIAC – Electro Numerical Integrator and Calculator – with its eighteen thousand tubes is over a thousand times faster than the relay machines, which in turn were twelve times faster than the original punched card machine at Harvard. This tremendous increase in speed is the result of shifting over from the use of one gram relay armatures to the use of 10^-31 gram electrons as moving parts. Of course a number of new problems appeared when this one limitation was removed. They are being cleared up one by one, chiefly by electronic means.

The ENIAC, despite the light weight of its moving parts, is no vest-pocket machine, as the number of vacuum tubes would indicate. The filaments of these tubes alone require eighty kilowatts of power, and a special blower system is needed to take away the heat. The whole machine occupies a space about 100 feet by 10 feet by 3 feet. Tube failures were a source of a good deal of trouble, because for while at least one of the eighteen thousand tubes burned out each time the power was turned on. This trouble was reduced by leaving the filaments of the tubes on, night and day, to eliminate the shocks involved in heating and cooling, so that now the ENIAC burn-outs at only about one per day, which take on the average of only fifteen minutes to repair. Experience with this machine has aided the design of a series of successors, such as the EDVAC, the UNIVAC, and the MANIAC – inevitable name.

The most important type of unit in the ENIAC is a device which uses two triode tubes, called a flip-flop circuit. These tubes will do electrically what the relay does mechanically. Normally one of the two tubes is conducting current, and the other is “cut off.” A very short – 0.000001 seconds long – pulse of voltage can cause this tube to cut off or cease to conduct, and the other to begin to conduct. Since only these two stable states are possible, we have the beginning of a binary computer. We must add a small neon bulb to indicate when the second tube is conducting, and then add as many such units in series as there are binary digits in the number we wish to handle. These circuits are used as a fast memory device. The ENIAC has a fast memory of only twenty ten-digit numbers, a serious limitation which can only be overcome by adding to the already large lumber of tubes, or by going to other types of fast memory.

Adding is accomplished by connecting flip-flop circuits in tandem so that they can count series of electrical pulses. This counting works in the same way that the mileage indicator works in a car, except that the scale of two is used. Thus, suppose that initially all our flip-flop circuits are in one condition – call it flip. The first pulse causes the first circuit to go from flip to flop. The next one will return it to flip, and this causes the first circuit to emit a pulse which sends the second circuit to flop. This continues on throughout the chain of circuits, all connected in tandem, as long as pulses are fed into the first circuit. When two series of pulses have been fed in we can get our number by noting which circuits are on flip – binary zero – and which on flop – binary one. The result may be converted back to pulses for use elsewhere. The speed per digit in the adding operation is a comfortably short ten microseconds.

The description of the adding scheme above has omitted one added complication in circuit design which gives a considerable simplification in reading of numbers. The binary system is used to count only to ten in the ENIAC and the number is then converted to a decimal number. This is a bit of a nuisance, circuit-wise, but handy – the decimal system is familiar.

The ENIAC also has electronic circuits for multiplying, dividing, square-rooting and so forth. The multiplier uses a built-in electrical multiplication table to aid it in its high-speed, ten digit operation. One very important unit in the ENIAC is the master programmer, which changes the machine from one computing sequence to another, as a complex computation progresses, in accordance with a pre-set plan. The master programmer even makes possible connections which enable the machine to choose the proper computing sequence when faced with the necessity for a choice. Thus it would almost seem that the machine does possess a kind of built-in judgment, and that there is some reason for the term “electrical brain.”

It was mentioned that the fast memory of the ENIAC was limited. The slow memory, using punch cards, and IBM machines causes a great reduction in speed when it must be used. Also, although computation is all-electronic, data is fed in and results are taken out by electromechanical means – punch cards again. The limitations incurred may best be realized if we compare the time for a punch, about half a second, with the unit time of a flip-flop circuit, ten microseconds. The ratio is fifty thousand times.

Even more serious is the problem common to all digital machines, namely the difficulty of setting up a problem. These machines are not easy to use, and the sequence of operations for an easy problem may be very involved. If the problem is difficult, then, of course, the sequence gets more difficult, but the use of machine methods is mandatory. So, when faced with a real stinger of a problem, the scientist gets down to work, perhaps for months, just to figure out how to set up the machine. Considerable time is needed for the physical setting up of sequence connections too, but after that – brrrrrrrrrrrrrp, and a solution which would take years by former methods begins to roll out in a matter of minutes.

Professor D.R. Hartree of England, who recently worked with the ENIAC, describes the solution of problem in which this machine had to handle two hundred thousand digits. Now try writing digits as fast as possible. At a rate which will lead to errors and writer’s cramp you may put down ten thousand digits in an hour. Even at this speed it will take twenty hours just to write down two hundred thousand digits – and no computation has been performed. The machine handled the numbers and performed the computation in this example in four minutes flat. It is not surprising that Professor Hartree is impressed by such speeds – he once spent fifteen years on the computation of the electron orbits of atoms. This is the kind of job that a machine calculator can be coerced into doing in a few hours, or days at most.

Their utility to science is obvious!

The ENIAC is only the first of its kind. The EDVAC – Electronic Discrete Variable Computer – is an improved machine, also built Army Ordnance at the r of Pennsylvania. One of the chief improvements is a larger capacity memory device, made possible use of acoustical delay lines for storage of numbers. Numbers get stored as trains of compression pulses is bouncing back and forth in a two-inch column of mercury. Each delay line of this type does the work of five hundred fifty electronic tubes in the ENIAC, so that a substantial saving results.

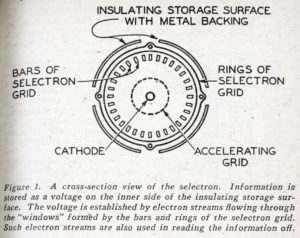
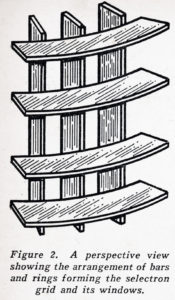
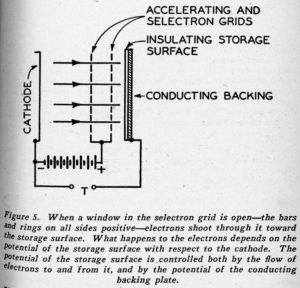
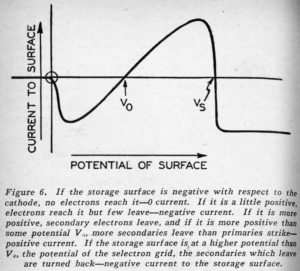
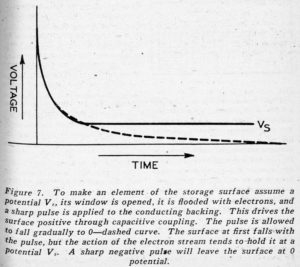
The MANIAC – Mechanical and Numerical Integrator and Computer – is another Army Ordnance computer. It is being built at the Institute of Advanced Study at Princeton under the direction of Dr. J. von Neumann and Dr. H.H. Goldstine. This machine is to use a new type of fast memory tube which is being perfected by Dr. Jan Rajchman of RCA. This tube, called the Selectron, is a kind of cathode ray tube which is designed to store four thousand ninety-six off-on or binary signals – equivalent to about twelve hundred decimal digits. The binary digits are to be stored as charge on points on a cathode screen which are behind the interstices of two orthogonal sets of sixty-four wires each. An ingenious method of connecting certain of these wires together will enable electric signals to be fed in to pull the electron beam to any position for purposes of reading” or “writing” with just thirty-two leads brought out. Even so a pre-production model of the tube looks a bit formidable, but it is phenomenally small for the memory it possesses.

Among some of the other schemes for digital memory being worked on are delay networks using loops of wire in wire recorders. This scheme may not be as fast as the acoustical delay line used in the EDVAC, but it has the advantage that the pulses do not have to be periodically removed for reshaping. One practical difficulty here is the necessity of waiting for the right point on the wire to come around before reading begins. Of course all memory of a number can easily be erased when need for it is finished, and the wire loop is ready to be re-used.

It seems that the Selectron is one of the best bets to speed up the operation of all-electronic computers. With its aid it should be possible to multiply two twelve-digit numbers in one hundred millionths of a second.

Such speeds may seem fantastic, but problems have been formulated and shelved because even the fastest present-day computing machines could not complete the solution in thousands of years.

The Bureau of Standards, aided by Mauchly and Eckert of ENIAC fame and others, is now constructing some new machines of a general purpose type. This new digital computer is called the UNIVAC – Universal Automatic Computer – and is to be of a general purpose type suited for Bureau of Census work as well as, Army and Navy ballistics and fire control research. The UNIVAC is to be very compact, using only about eight hundred tubes, and occupying only about as much space as five file cabinets.

It is rather interesting that one of the limitations of this and other digital machines is the slow rate at which numbers are printed at the output. This limitation may be overcome in future machines by the use of a device called the “Numero-scope,” recently announced by the Harvard Computation Lab. This device is nothing but a cathode-ray oscilloscope, which can trace the outline of any number, if the right signal is fed into its deflecting plates. This is no mean trick – it takes six vacuum tubes to make the numeral 2, for example, but it has been done, and numbers may now be flashed on the screen of a cathode-ray tube and photographed with exposures as short as one five-hundredth of a second.

The analogue computer, as we have stated works with analogous quantities rather than with whole numbers. Thus we may represent quantities by lengths, angles, voltages, velocities, forces and so on. Thus an electrical or an hydraulic circuit problem may be solved on a mechanical device, while an electrical problem may be solved on a mechanical device. One simple example of an analogue computer is the slide rule. Here quantities of any sort are converted into lengths and since a logarithmic scale is used it is possible to multiply by adding lengths. If a linear scale is used we can add by adding lengths. Division and subtraction are possible by simply subtracting lengths in each case.

__________

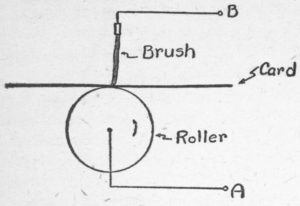
The basic mechanism in the punched-card machine is the brush and roller combination shown. As the card passes over a steel roller, metallic brushes make an electrical connection – between A and B in the diagram – and a signal can be produced to reject the card, or set a counter wheel, et cetera.

__________

If we use angles, or angular displacements, to represent quantities successive displacements readily add to give a total. We can also use a differential like the one in the rear end of a car to add the angular displacements in two different shafts. The answer in this case, or a constant factor – gear ratio – times the answer appears on a third shaft. Direct voltages add conveniently, and alternating voltages add like vector or directed quantities, and so are convenient in the solution of problems involving directed lengths or forces.

Before going any further into discussion of the specific details or these devices it might be well to examine the relative advantages and disadvantages of the analogue type of computer. In the digital computer the accuracy can usually be increased at the expense of speed, so that if we want to go from 10 digit to 20 digit accuracy we must suffer a decrease to half the original speed.

With the analogue type of computer it is only possible to increase accuracy if the lengths – or angles, or voltages, or whatnot – are measured with greater percentage accuracy. This may call for watchmaker techniques unless we can afford lengths or other analogous quantities. The difficulties encountered in any case are such that the accuracy is always much less than in any digital machine.

There are several advantages possessed by the analogue computer which tend to offset the decreased accuracy. One of these is its greater speed, which results partly from the fact that most problems are more easily set up for solution by analogue methods. Sometimes the analogue computer is used for a quick look at a problem, to narrow down the field which must be investigated with greater accuracy by the more involved digital computer. Another advantage possessed by the analogue computer is its ability – if the ability is built in – to perform certain mathematical operations in direct fashion. Thus, for example, a pivoted rod can be used to give the sine of an angle. This ability also accounts in part for the greater speed by the analogue method. Still another advantage is ease with which empirical data in the form of curves may be fed into an analogue machine.

The first successful large-scale analogue computer was the Differential Analyzer designed by Dr. Vannevar Bush and others at M.I.T. The same type of machine has also been built by General Electric for its own use and for use in various Universities. The latest and most highly improved of these machines was recently installed at the new engineering school at U.C.L.A.

____________________

“1948-08-06: UCLA’s Differential Analyzer Begins Rise to Stardom“, at TomOwens YouTube channel.

Note that this YouTube clip shows the incorporation of the differential analyzer in the movies When Worlds Collide, from 2:00 to 4:13 (full length version here), and, Earth Versus the Flying Saucers, from 4:36 to end (in full-length version at Archive.org, from 59:28 to 107).

____________________

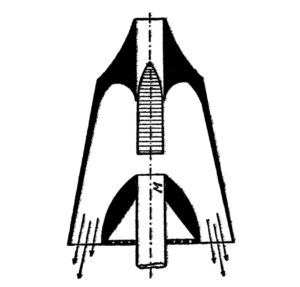
The differential analyzer is used chiefly for the solution of differential equations. In view of this fact it is rather strange that the machine cannot differentiate. However it can integrate, and since this is the inverse of differentiation its mastery over the calculus is quite complete. (The inverse of an arithmetical process is commonly used by clerks in stores who count back our change, and thus use addition in place of subtraction). The integrators in a differential analyzer are of the Kelvin wheel-and-disk type in which an integrator wheel rides on a rotating disk, and is turned when the disk turns. The amount of angular rotation of the integrator wheel depends on its distance, R, from the center of the disk, and the angle the disk turns through, θ. This, by definition, is the integral of R with respect to θ.

The integrator is the most important device in the differential analyzer, and as such has received a great deal of attention. In 1944 G.E. engineers came up with a device in which troubles caused by slipping of the integrator wheel on the disk were virtually eliminated. This device was essentially a servo follow-up system in which light beams were passed through a polaroid disk attached to a very light integrator wheel. These light beams then went through other polaroid disks, then to phototubes, to an amplifier and a motor. The motor then caused the second and third polaroid disks to follow the disk on the integrator wheel with the customary boost in power level, or torque level.

Among other important components in the differential analyzer are the input tables. At these tables, in the older machines, operators followed plotted curves of functions which were to be fed into the machine with pointers, and thus converted distances on the curve sheets to angular rotations. In the newer machines light beam photocell servo-mechanisms accomplish the same thing without the aid of skilled operators. Known functions, of course, are generated by other and simpler means.

Because the differential analyzer handles quantities in the form of angular displacements the process of adding is accomplished by the use of differential gearing. To solve a differential equation the machine must first be set up so that the right shafts are connected together by the right gear ratios. When all is ready the data in the form of curves is fed into the machine at the input tables, the known functions are fed in from function generators, and the output pens are moved from left to right, all in synchronism. Adding wheels, integrators, input table lead-screws and so forth all begin to move and perform the operations required by the equation being solved. The totals of the quantities on each side of the equation are held equal by a servo-mechanism and the shaft which will give the function which is the desired answer moves the output pen up and down as it is pulled across a sheet of graph paper. Thus the answer appears as a curve, or a set of curves.

The accuracy of these results depends not only upon the accuracy with which these final curves can be read, but also upon the accuracy of the original data, and the accuracy of the various servos involved in the solution. Typically, about one-tenth of one percent, or three digit accuracy can be expected. If some of the components have been forced to accelerate too rapidly because of a poor choice of gear ratio, or if a lead screw has been forced to the end of its travel, the solution may be completely wrong – the analyst still has his headaches. These troubles are ordinarily avoided by making preliminary runs to determine the proper ranges of operation of all components.

Among the other types of analogue computers commonly used engineering work are the various kinds of network analyzers. A large electrical power network may be exceedingly complex, due to the more or less random geographical distribution of loads and generating plants. The effect of short circuits, arc-overs due to lightning, and load distribution must be studied with the aid of models, so that the design of circuit breakers, lightning arresters and so forth can proceed intelligently. Tests cannot be made on the actual power network, as they can on communication networks, because of the possibility that damage to large and expensive equipment might result.

The earliest type of power network model was the D-C Network Analyzer. The representation of three-phase alternating current systems by direct-current models of this kind has definite limitations, and the next step was the development of A-C Network Analyzers. These models, although they represent a three-phase system by a single system are much more versatile than the D-C Analyzers.

We may ask if such models should really be classed as computers. Fundamentally, these analyzers are merely models of systems which are too complicated for direct analysis, and too large for direct measurement of variables under all possible conditions. Much the same kind of model-making is carried on in the study of aircraft antennas using model planes and microwaves in place of short waves. However, if we examine some of the uses to which Network Analyzers have been put, it seems safe to class them as computers. Because of the use of electrical quantities in these devices and because of the flexibility of interconnections possible, they have been used for the solution of such problems as the flow of microwave energy in wave-guides, the flow of compressible fluids in pipes, and even the solution of Schrodinger’s Wave Equation.

Another type of network analyzer is the Transient Network Analyzer, which can show more clearly what happens in a power network when short circuits and overloads occur. This device may also be used to study analogous problems such as the amplitude of transient vibrations in mechanical systems when sudden shocks or overloads occur. The inverse of this kind of thing is the mechanical model used to study what goes on in a vacuum tube. In these models stretched sheets of dental rubber are used to represent electrostatic fields, and ball bearings serve as electrons.

The differential analyzer is more versatile than the network analyzer discussed above because it can integrate, differentiate – in effect – and multiply, and thus solve rather complicated differential equations. These functions are performed by mechanical or electro-mechanical devices in the differential analyzer. If these things could be accomplished by purely electrical means, we would expect a great increase in speed, and some decrease in size and weight. Such machines have been built by Westinghouse and Caltech, and seem to promise a fair increase in speed over the old differential analyzer. It seems inevitable that the use of many vacuum tubes will lead to somewhat lower accuracy and less dependability. Another difficulty with present types of electronic differential analyzers is that integration can only be performed with respect to time as the independent variable, so that the solution of certain problems is not easily possible.

Many other kinds of analogue computers have been perfected in the last few years – the field is definitely “hot.” Completed designs include such gadgets as the Bell Telephone M-4 Director, which used radar signals to figure out in a twinkling where an antiaircraft gun should be aimed so that the shell and a plane might meet. Undoubtedly work is in progress on computers which will make possible solution the “problem of delivery” of the modern atomic warhead. These latter-day buzz-bombs will be sufficiently lethal to warrant their carrying along their own computers.

Many scientists are disconcerted by the fact that by far the greater part of the computer research being carried on today is under the auspices of the Armed Forces. To be sure, we in the United States seem to be far ahead of anyone else in the world in computers. This may augur well for National Security if some desperate bludgeoning struggle is soon to occur. From the longer range point of view it seems that it is particularly desirable that the scientist whose pure research may lead him to yet undiscovered fundamental truths be also equipped with this new and powerful tool.

__________

Three types of computers. Top: General Electric’s A.C. Network analyzer. Middle: The differential analyzer – of the analogue computer group – at General Electric. Bottom: The Bell Laboratories relay-operated digital computer.

References and Suggested Readings

Network Analyzer (AC power), at Wikipedia

Differential Analyzer, at Wikipedia

The UCLA Differential Analyzer: General Electric in 1947, Video at Computer History Museum

“The Differential Analyzer. A New Machine for Solving Differential Equations”, by Vannevar Bush, at WorryDream

Differential Analyzer History, at LiquiSearch.com

A Brief History of Electrical Technology Part 3: The Computer, at Piero Scaruffi’s website

War in Space, 1939 – III: “Space War Tactics” in Astounding Science Fiction, by Malcolm Jameson and Willy Ley (1939) – Readers Respond

The appearance of Willy Ley and Malcolm Jameson’s articles about Space War in the August and November issues of Astounding Science Fiction for 1939, generated – unsurprisingly – a small fusillade of laudatory comment in the magazine in its issues of October and December, 1939, and May of 1940. The contributors were Thomas S. Gardner of Kingsport, Tennessee; A. Arthur Smith of Ontario, Canada; J.M. Cripps of Manhattan, Kansas; James S. Avery of Skowhegan, Maine, as well as Jameson and Ley themselves, in the October and May issues, respectively.

In the October issue, reader Gardner gives his evaluation of the literary merits of the August, 1939 issue, and follows with agreement about Ley’s article, albeit suggesting that “rays” might be safer weapons than projectiles, albeit not explaining how. Malcolm Jameson’s letter provides insight into his career in the Navy. Then, he segues into the “core” of his own article, which pertained to locating, tracking, and aiming at an enemy spacecraft. He also addresses the technology of guns, or more accurately, cannon, in terms of the weight (mass) of the gun itself, qualifying this with the realization that his comments pertain to guns in terrestrial conditions, not space.

Reader Cripps, in the December Astounding, turns out to be an advocate of “rays”, under the proviso that, “if you [Willy ley] admit-their scientifictional credibility, it won’t strain you too much to realize that there is just a possibility that those same projectors might not be either so weak or so sensitive to shaking or jarring as you seem to think.” He premises this on the assumption that spacecraft can be propelled – be powered and reach escape velocity; leave a planet’s gravity well – solely by means of “ray projectors”, rather than, “the sort of chemical rocket that can he designed today.” In this context, he suggests that energy released from a cyclotron could be transformed into electricity and then projected into space via a “ray generator” or “refractory projector”, without (!) expanding onto how said generator or projector is specifically to function.

Well, feasible or not, it’s interesting to think about!

As for addressing Willy Ley as “Herr Ley”? Whether that is a sign of respect, or something else again, will remain unknown…

In the issue of May, 1940, reader Avery’s comments parallel those of Gardner in 1939, addressing the magazine’s literary content, and positing a question concerning Jameson’s analysis of a spacecraft versus spacecraft battle. Then, Willy Ley explains his advocacy of guns versus “torpedoes”, by focusing on the suitability of 37 and 75mm canon, specifically in terms of the weight of the former. As for the “37”, “…that they are effective enough has meantime been demonstrated by the new 37-millimeter anti-tank guns of the U.S. army that “disintegrated” 1 ½-inch steel armor plate at a thousand yards without a moment’s hesitation. That 1,000 yard range means, of course, in air – for space conditions it might safely be multiplied by a hundred or even more.” Perhaps so for space warfare. However, in terms of (terrestrial!) anti-tank combat, while the 37mm (M3) gun was a suitable weapon against pre-war tank designs, Japanese tanks throughout the war (in a general sense), and light (including German) German armored vehicles, it was not an effective weapon against the Panzer IV and later German tanks.

Anyway, to liven things up a little bit, included are images of the covers of the relevant issues of Astounding, those for October, 1939 and May, 1940, having been found on the Internet. There is also a lovely piece of black & white interior art, I’m certain by Henry Richard Van Dongen.

Astounding Science Fiction

October, 1939 (pp. 154-160)

Malcolm Jameson plans to expand on Ley’s ballistics!

Dear Mr. Campbell:

I regret to have to give Astounding Stories a very good rating for the August, 1939, issue. I repeat, I regret, because it is very difficult to keep up such a high standard as Astounding has been setting for the past six months. I am afraid that I will be disappointed one of these issues — although I know that you will do every-thing to prevent such a catastrophe. Now to business:

Cover – good. It strikes a note of action and force. I like the contrasting reds and darker colors.

Your little editorials are quite Interesting – in spite of the fact that sometimes I do not always agree. However, this month we agree.

“General Swamp, C.I.C.” Quite a good and logical story – parallels the American Revolution. Your characters are well drawn, and I am glad to see the individualism shown, for it is passing out in America now. Of course, it is harder to fight a war with people who are free individuals – as we found out in 1776.

“The Luck of Ignatz” – A good character, I should like to see more of this character.

“The Blue Giraffe” – Humor can be used well in s-f. and de Camp handles it best of any that I have seen.

“Pleasure Trove” – The type of story that made old Astounding under Clayton liked – scientales with a punch. Thanks for the breathing spell from the heavy stuff.

“Heavy Planet” – Good. A logical and well-handled situation.

“Life-Line” – Very plausible and better on the second reading. The doctor didn’t completely believe his own theory and proof until he failed to save the young couple – then he knew that his own time was about up and he couldn’t change the future. That was cleverly put in the story.

“Stowaway” – Fairly good story and a good poke of fun at Earthlings.

“An Ultimatum from Mars” – The best of Cummings that I have seen in a long time.

“Space War” – Fine. Willy Ley sure knows his engineering and some ballistics. The article was the best of its type for some time. He is dead right – guns are going to be really tough to handle in free space. The trouble is in hitting the object – a whole new science of ballistics will have to be worked out – something like the multiple body problem on a small scale.

Tell Ley that rays might be safer – it they are developed on a large scale due to their spreading – for space around a battle will be uninhabitable for long distances due to unexploded bombs, et cetera. Of course, the h.e. shells will travel far away if they don’t hit.

Inside Illustrations – I still like them O.K.

General make-up was O.K. So you see why I regret to have to give it such a good rating – for can yon repeat next month? I hope so. – Thomas S. Gardner, P.O. Box 802, Kingsport, Tennessee.

SCIENCE DISCUSSIONS

Malcolm Jameson is one of the country’s few real experts on really heavy guns.

Dear Mr. Campbell:

Up to now I have been one of the most inarticulate of your contributors, but Willy Ley’s “Space War” in the August Astounding, is like smoke in the nostrils of an old fire-horse – it starts me itching to hop into the ring with him for an unlimited bout where we can hurl back and forth the fascinating facts of ballistics – both interior and exterior – and drag in that other science that utilizes both of them and some other things – Fire-Control. Ordinarily, I approach your science articles with a good deal of deference and with appropriate modesty, but when anybody starts writing about ordnance he is on ground where I think I know my way around. It happens that I spent eight or nine of the best years of my life where ordnance was being designed, manufactured, tested and used – in gun factory and laboratory, at proving grounds and on warships, both in peace and war, and in the field with troops. So if I make bold to comment: on Mr. Ley’s article, it is because I feel that I am competent to do so.

Not that I mean to imply I have fault to find with it. On the contrary, I am all for him – barring a few minor points. I like his demolition of the heat-gun and ray-screen doctrines, and the way he sails into other fantastic gadgets. I am in thorough accord with his choice of propelled explosives as the most probably final weapon of future warfare. My chief criticism is that he did not go far enough. He tells us what projectiles will do to the hostile ship, but not how to find it and hit it. The problem of finding the enemy and maintaining contact long enough to hit him, considering the stupendous reaches of the void and the colossal speeds involved, seems to me to transcend all other considerations. But then, that is the subject matter for another article entirely.

It occurs to me, however, that readers of Astounding may be interested in some expansion of several of the things Mr. Ley mentions; and also I would like to take issue with him as to one or two of his statements. Merely to list and briefly describe the many known factors that enter into gunnery would require pages, so I will confine myself to a few of those touched on in the article.

He spoke of the retarding effect of the air in the rifle bore ahead of the projectile. I can cite an instance that illustrates that beautifully and it won’t be necessary to swamp you with graphs, formulae or statistics. When the battleship Mississippi went into commission, Dr. Curtis of the physics department of the Bureau of Standards was one of the experts who went with us to Cuba to hold her experimental battery tests. Among other things, he desired to measure muzzle velocity under shipboard conditions. M.V. determination up to that time had been done only at the Proving Ground where it was possible to fire the shell through two successive screens hung in front of the gun.

Dr. Curtis rigged two metallic fingers at the muzzle of the gun, protruding slightly above the bottom of the rifling grooves, and also stretched a wire across the bore opening. These were parts of two electrical circuits, each hooked up to oscillographs. The idea was that the nose of the emerging shell would break the wire, thus interrupting one current, and that the bourrelet, or rotating hand, would wipe the fingers and complete the circuit of the other, thus producing two wiggles on the oscillograph tracing. He knew, of course, the exact distance from the shell-top to the lending edge of the bourrelet.

The first readings were absurdly low and Dr. Curtis correctly guessed that it was because the outrushing air had broken his wire before the shell got there. He put in heavier wire. Then a steel rod. Believe It or not, it was not until he had worked up to an iron bar, of something like 3/8 of an inch by a couple of inches, set edgewise like a girder across the opening, that he found something that would stay there until the projectile emerged. Even at that he had trouble with its fastenings. Some breeze!

I note Mr. Ley’s complaint that designers simply do not pay attention to weight unless the question of transport is involved. I assure him he Is quite mistaken. If the guns of a battleship could be reduced in weight by so little as five per cent, it would mean the saving of many tons which could well be utilized for other purposes. Actually, other characteristics of the gun being equal, gun weights have steadily declined – due chiefly to improvements In steel-making processes, notably heat treatment. Presumably, the trend will continue as better methods and stronger alloys are found.

The reason for the present weight of guns is stark necessity. It takes a lot of metal to withstand a suddenly applied force of upward of twenty tons to the square inch. When he says that reducing the thickness of gun barrels shortens their service life, he is dead right. It shortens it all right – is likely to cut it down to one terrific and fatal blast. If he had had the opportunity as I had, of seeing many ruptured field guns lying on Southampton dock during 1917, he would not think the factor of safety overstressed.

As to the difference in thickness between a worn-out gun and a new one, it is almost imperceptible to the untrained eye. Gunners keep a careful record of the number of rounds fired and star-gauge their guns often, for that is the only way they can keep track of the erosion. A worn bore, and the wear may not exceed the thickness of this sheet of paper, permits the powder gases to escape past the projectile, thereby seriously reducing its velocity. It also fends to promote wobble in flight.

In the vicinity of the breech not only are the pressures greater, but the temperatures are terrifically high, and I suspect that the lining of the powder chamber and the face of the breech-plug is for a moment In a virtually molten condition. I witnessed a blowback once, through an infinitesimal hairline scratch on the seat of the gas-check seal. It was a brand-new 14” gun under proof and the breech of it was ruined. The gases escaping through that little hole blew I the metal out in a line spray, like butter under a blow torch. Of course, the speed of the leaking gases added vastly to the damage, but it must be hot in there.

I doubt very much whether a strictly non-recoiling gun is possible. The recoil begins much earlier than most people Imagine – shortly after the projectile has started moving within the barrel.

In regard to the “optimum” elevation of 45 degrees, I might say that that is the elevation that theoretically gives the maximum range. I have seen heavy guns fired all the way up to fifty degrees, but there is little gain in range after the upper thirties, and a progressively greater loss of control. The famous German long-range gun could only be effective against a target as large as the city of Paris. Hitting somewhere within a ten-mile circle is not an artilleryman’s notion of marksmanship.

As to streamlining, that has been tried but is not practicable for several reasons. However, that does not mean that the shape of the shell is unimportant. The “coefficient of form” is an important one; long-pointed shells travel farther than short blunt ones. Armor-piercing projectiles that have to be stubby are equipped with false noses for that reason.

Of course, I realize that all this quibbling is about Earthly conditions and is not very applicable to what happens in the void. I am writing only because It may be of interest to our fans. As to the extension of Space Warfare to take in such matters as scouting, range finding, tracking and spotting, I am very much tempted to break out as an article writer myself. Then Mr. Ley can slip in a new ribbon and do a little sniping of his own. – Malcolm Jameson, 519 West 147th Street, New York, N.Y.

Maybe you can use rays, at that!

Dear Mr. Campbell:

I want to make a few comments about the August number of Astounding.

First point is Willy Ley’s article on the weapons of space combat. Frankly, I’ll still stick to the flaming rays and scintillating screens; Mr. Ley’s argument against them starts off with a bit of a self-contradiction. On page 74 he states: “That they (ray projectors) do not exist now is immaterial; science-fiction is not only concerned with things that are, but also with things that might be.” And forthwith proceeds to argue them out of existence on the grounds that the equipment necessary to produce them would be so ponderous compared with present-day artillery as to make them impracticable. Come, come, Mr. Ley! Surely, if you admit-their scientifictional credibility, it won’t strain you too much to realize that there is just a possibility that those same projectors might not be either so weak or so sensitive to shaking or jarring as you seem to think.

You say the projector would need a power plant, and “power plants are notoriously heavy.” O.K. But it also appears to me that even an unarmed ship might need a fair-sized set of generators just to lift it into space; unless, of course, you insist on limiting the poor writer to the sort of chemical rocket that can he designed today.

You say that the ray generator would be sensitive, “since we have to assume tubes of some kind.” Do we, now? Let’s try a spot of assuming, and see what sort of power plant and ray projector we can dream up, even without going too far beyond our present scientific knowledge.

Power plant first. Suppose we make it an atomic energy set-up, using the fission of uranium 235 under neutron bombardment. We’ll need a source of neutrons to start off that reaction. Cyclotron, perhaps, since you seem to like a heavy power plant; though I think that with U-235 a simple, light, insensitive radioactive source might work as well. A cyclotron would have tubes to go out during an engagement, all right, but we needn’t worry about that; we’ll just use it to touch off the process at the start, and keep steam up afterward, since the reaction is self-perpetuating. Probably need a direct hit now to put that job out of action.

Ray projector? Well, I suppose we could turn the released energy into electricity, to be later transformed into some deadly radiation In a delicate ray generator. It seems to me that a stream of those 200-million-volt atomic nuclei given off by disintegrating uranium, and released in the general direction of the enemy through refractory projectors would be just as deadly and a lot simpler. That question of refractories Is a delicate one, I admit; but we’ll need them, anyway, for the power plant, so let’s not strain at gnats while swallowing camels.

Do I hear an objection from Mr. Ley? “If there is an insulating material that holds out against the energies released at the giving end, it is hard to understand why the same insulator should not be usable to safeguard the bull of the ship that is being rayed.”

Same answer as to the question : Why not armor-plate the ship against solid and explosive projectiles from Mr. Ley’s heavy artillery? Too heavy; and, perhaps, a whole lot more expensive than even the best nickel-steel armor. But if you insist, I’ll make my ship invulnerable to ray attack; only you’ve got to reciprocate, and turn yours into a flying fort, complete with 30-inch plate all round.

This begins to look like stalemate. So let’s compromise; fit out our warships of space with both rays and guns, ray screens, insulation, and armor-plate, and see what new forms of deviltry the boys can think up with that equipment.

It should be interesting. – A. Arthur Smith, 131 Aqueduct Street, Welland, Ontario, Canada.

Astounding Science Fiction

December, 1939 (p. 108)

To the defense of rays.

Dear Sir:

As a rule, your stories are good and your articles better; the article entitled “Space War,” by Wily Ley, is however, the exception that proves the rule.

Before I attempt to back up the above statement, perhaps I had better give my qualifications. I have some sixty-odd hours of college chemistry, twenty-two hours of college physics, and thirty-four hours of college math. I spent three years in the National Guard attached to a battery of 155 mm guns.

I am too lazy to attempt to check Herr Ley on his statements of armor weight, gun weight, et cetera, but they seem reasonable, so I will allow them to stand without argument – they would probably stand, anyway.

Taking up Herr Ley’s arguments in order, I wonder if it ever occurred to him that it would require quite a good power plant to lift a “fair-sized spaceship, about ninety yards long and twenty yards in diameter,” from the surface of the earth and then set it gently down again? It seems to me that the weight of the mechanism required to divert part of this power from drive to ray generator would not be prohibitive. Vacuum-tubes are delicate, but could be made stronger if necessary, and, if not, I believe would rather risk having a tube blow during the course of a battle and leave me without effective weapons than to have an enemy shell land in the ship’s magazine.

He kindly granted the possibility of dangerous rays and then stated that he did not believe they could be developed in the near future. Micro-waves – radio – from 30 cm. down in wave length would be quite disconcerting if there were some 50,000 watts being fed into them. You see, they are picked up by a metallic conductor as heat. They may not be what the science-fiction author has in mind when he refers to heat rays, but they’ll work quite nicely, I believe, and they focus into the neatest tight beam. As for ray shields, there is always heterodyning.

As to the impossibility of “holding a ray on a fast-moving distant target, that might be practically invisible with black paint against the background of black space,” just how many men could hit a black disk twenty yards in diameter on a dark night such a range and moving with such a velocity that a searchlight – just another ray – could not hold it?

In space a heat ray is an accumulative affair in that heat is dissipated only by radiation, which is a notoriously slow process at ordinary – 0-200 C-temperatures. This would mean that the heat ray would not have to be held on the target.

As for the disadvantages of guns, Herr Ley has neglected to mention that in warfare on earth, when a heavy gun is firing at a target the gun is relatively motionless with respect to the target. This simplifies aiming considerably. Dog fights between planes are never long-range affairs because of their relative velocities. Going back to ground fighting, however, a miss of twenty yards or so is as good as a hit because of the bursting range of the shell. A miss of one cm. in space is as good as if the shell had not been fired.

When Herr Ley advocates the use of 75s in space, it is obvious that he has never been around them when they were fired. I have, and I wouldn’t care to be in a closed room – even if it were evacuated – with one firing several rounds to the minute.

During the World War gas was used frequently so as to force the men to don gas masks. The masks cut down the firing efficiency noticeably. I wonder when effect a space suit would have on accuracy?

The science of exterior and interior ballistics is built around the presence of air and a fairly strong gravitational field. It would take some time to develop a science of vacuum ballistics.

Reading this over it appears that I have laid the foundations – or destroyed them – for a good way – right here on earth between Herr Ley and me. I’ll try to prepare myself for his counter-attack, because I don’t believe I destroyed him entirely. – J.M. Cripps, Manhattan, Kansas

Astounding Science Fiction

May, 1940 (pp. 159-161)

Yes, but who’s going to use a slow spaceship if the enemy has fast ones?

Dear Mr. Campbell:

It seems now that the latest vogue in science-fiction stories is that of rocket-racing, and it is only natural that you should secure the best of that type yet published. By this, I refer to the clever and well-written “Habit” by Lester del Rey in the November issue. This excellent little piece has that “certain something” that sets it off as a typically Astounding story. I honestly believe that were I given an armful of untitled, anonymous, and as yet unpublished manuscripts, I could tell within ninety percent or better which would find refuge in Astounding and which would go to your umpteen competitors. It’s style, not plot, that makes Astounding the “class magazine” that it is.

May I add a line or two to the rumpus stirred up over the merits of the “General Swamp” serial. To my mind it ranks with the best of any two-part serial yet published. Its handling was so uniquely different that it captivated me from the very start. It was realistic to the point of having me half believe I was reading actual reports and military accounts! Kick on the hard-to-pronounce names? Not me! surrounded as I am by left-over handles of the Indian period – Skowhegan, Messalonskee, Norridgewock, Kennebec, Mooselookmeguntick, Cobbseecontee, et cetera. How does Arkgonactl and Golubhammon compare with these?

Space war articles and letters by Ley and Jameson appeal greatly to me, despite the fact that they hopelessly destroy – and quite logically, too – my pet dreams of flashing ray battles In the void. But wouldn’t two ships traveling a parallel course at equal or near equal speeds be visible lo one another? Jameson seems to think not. Also comes up again the slow-speed spaceship theory that blasts the seven-mile-per-second principle – page 70 of “Space War Tactics” – off the records. Still, Jameson accepts that, too, … – James S. Avery, 50 Middle Street, Skowhegan, Maine.

SCIENCE DISCUSSIONS

Experts transposed?

Dear. Mr. Campbell:

That the problems of spate war and space war tattles are infested with wide gaps of knowledge and with difficulties of all kinds is proven by one fact: I recommend guns, while an old gunnery expert like Malcolm Jameson prefers rocket torpedoes! If it were the other way round, nobody would be surprised.

My reasons for recommending guns were already stated in my article “Space War,” the principal one being that guns with ammunition are lighter and less bulky than rocket torpedoes, provided that an appreciable number of rounds is to be carried. And since my comparison was based on rocket’ torpedoes capable of attaining the same velocity as gun projectiles, I think that the argument is still valid, if the torpedoes were to attain higher speeds they would he still heavier and still bulkier.

Answering first to Mr. Jameson’s letter I hasten to assert that I do not think that the weight of large caliber guns could he reduced very much, unless by the use of new alloys. I was speaking of small guns, 75 millimeter and less, and I still hold that I am right. The new anti-tank guns in all armies prove that point; they are much lighter than anything built so far. (I may add that those of the Swiss army are also equipped with a recoil eliminator.) And that they are effective enough has meantime been demonstrated by the new 37-millimeter anti-tank guns of the U.S. army that “disintegrated” 1 ½-inch steel armor plate at a thousand yards without a moment’s hesitation. That 1,000 yard range means, of course, in air – for space conditions it might safely be multiplied by a hundred or even more.

As far as tactics of combat are concerned, I, having neither experience nor theoretical training, have to be quiet. I cannot help but feel, however, that the tactics of sea or aerial combat do not apply to a very great extent. We always have to hear in mind that an orbit in space and a course in air or on the high seas are not exactly the same. Spaceships are not steamers that travel at will, but rather canoes in swift and powerful currents. These canoes have paddled that permit some movement at will and some steering, and If the “currents” were not as regular and ad calculable as they are the case would be hopeless.

Spaceships, therefore, will either pass each other in opposite directions and at such relative speeds that hardly anything could be done, or else they will follow about the same course and by necessity have about the same velocity. It is the latter condition I had in mind, and it is in that condition where guns will he advantageous. Mine laying is, of course, a nice idea, but again I do not quite see why mines should be superior to guns, generally speaking. Mr. Jameson is trying to do something that is very hard to do when he proposes that the space mines, or iron pellets, should be “shot out of mine-laying tubes clustered about the main drive jets. They would be shot out at right angles – and given a velocity exactly equal to the ship’s speed, so that they would hang motionless where they were dropped. The latter does not hold true exactly; the pellets would at once start moving in the general direction of the Sun – If they are exactly motionless it would be the exact direction toward the Sun – but since that movement would he very slow at first and the enemy ship reaches the area of the mine field In a few seconds, that factor can he disregarded. What bothers me is the problem how the mines could be shot out with a velocity exactly equal to the ship’s speed. That speed is assumed to be about 20 – 25 miles per second. Muzzle velocities of guns will be between one and – possibly – one and a half miles per second. And even the gas molecules in the rocket exhaust do not travel faster than, say, three miles per second. If a method could be found to shoot the space mines away from the ship with 20-25 miles per second, that method should be applied to throw shells.

Since I have started criticizing other people’s Ideas, I might as well say a few words about Robert Heinlein’s enjoyable story “Misfit.” Generally speaking, I think that moving an asteroid for the purpose of using it as a station in space is a very wasteful business. It would take much less fuel to transport building material to the chosen spot in space from Earth or Mars. An asteroid possesses an awful amount of useless mass that has to be transported, and each pound of mass requires so and so much fuel. It Is somewhat like moving a large mountain from one continent to another because there is a forest growing on top of the mountain and the larger trees of that forest are to be used to build a raft.

But even if we concede lo the waste of fuel to move the asteroid, there Is no reason to waste more than half of that fuel in giving “88” “a series of gentle pats, always on the side farthest from the Sun.” What has to be accomplished is to slow down the orbital velocity of the asteroid so that the gravitational attraction of the Sun gets the upper hand and draws it closer. Which is done most effectively in setting off the rocket charges in such a way that they point “ahead,” at right angles to the line drawn from the asteroid to the Sun. The resulting movement would be along an elliptical curve – somewhat distorted, to be sure – but not a hyperbolic curve. And there is no need for such unnecessary accuracy. If the asteroid should finally possess a few hundred feet of orbital velocity more or less, is really unimportant. It would make a difference of ten or twenty miles – or even fifty or a hundred – in the average distance from the Sun. There is no reason why that should matter, just as it does not matter whether an island in the Atlantic Ocean is half a mile farther west or not; it only matters that captains know where It is. Besides, the orbit of the asteroid could be corrected at any time, if desired. But I wouldn’t move asteroids at all.

I wish to say “thank you” to Mr. E. Franklin of Jamaica Plain for his nice and interesting letter in the October issue. The real trouble with articles is that they have to be shorter than the “Gray Lensman.” – Willey Ley, 35-33 20th St., Long Island City, N.Y.

War in Space, 1939 – II: “Space War Tactics” in Astounding Science Fiction, by Malcolm Jameson (November, 1939)

Deprecated: Function create_function() is deprecated in /home3/emc2ftl3/public_html/wp-content/plugins/wp-spamshield/wp-spamshield.php on line 2033

Three months after the appearance of Willy Ley’s article “Space War” in the August, 1939 issue of Astounding Science Fiction, Malcolm Jameson penned (well, in all probability, he typed – remember typewriters?) a follow-up article of similar length and concept, but focused on a different aspect of spacecraft-to-spacecraft combat: The actual tactics of battle. Thus, Jameson – perhaps reflective of his background as a naval officer – accords attention to the maneuvers utilized by opposing spacecraft, only later in his article discussing weapons, and unlike Ley, being an advocate of “rocket torpedoes”.

Jameson’s article is supplemented by two diagrams which illustrate the trajectories of opposing spacecraft engaged in combat. (You can see his signature at the lower right in each.) In both diagrams – here limited to two dimensions, and viewed from “below” – the track of “our” spacecraft is on the left, and the enemy ship to the right.

In the first diagram, our craft is on a straight trajectory, with the enemy ship taking an abrupt “right” turn at position “7”, the weapons employed by our spacecraft presumably being rocket-torpedoes.

In the second diagram, the pair of spacecraft are on a converging trajectory, the weapons being mines as well as rocket-torpedoes.

Paralleling my post about Willy Ley’s article about space war, here are some general “take-aways” from Jameson’s article:

1) Military conflicts, regardless of the era or the nature of weapons employed, can be expected to follow the same general principles. Thus, though “space” is by nature a setting different from arenas of battle in the traditional sense, the same concepts and assumptions can be expected to hold there, as well.

However, two primary differences stand out: “Space” differs from taken-for-granted terrestrial settings (any planetary setting, really) in terms of its (apparently limitless) extent, and, the speed of the craft involved. The implications and challenges of the latter, in terms of even the nominal possibility of maneuver, as well as locating, tracking, aiming, and firing at enemy craft, cannot be underestimated.

2) Given the speed of combat between spacecraft, gunnery computations (like Willy Ley’s August article, Jameson’s analysis is based on the assumption that spacecraft armament will comprise some form of weaponry firing either simple mass weapons or explosive projectiles, rather than an energy weapon of unknown design and function) will demand the use of a “differentia calculator”. Though he does not elaborate, Jameson seems to have been either anticipating or conceptualizing such a device as ENIAC (Electronic Numerical Integrator and Computer), the existence of which was announced to the public ten months after his death.

3) The spacecraft’s armament is simple, whether by the standards of the late ‘thirties or 2021: The craft shoots projectiles comprised of “a simple sphere of meteoric iron”. Due to the velocities involved, explosives are entirely unnecessary: The momentum of such a projectile is entirely adequate to damage or destroy an enemy spacecraft.

4) A substantial portion of Jameson’s text – specifically pertaining to Figure 1 – pertains to the manner in which “our” spacecraft will locate, identify, and track the enemy vessel, and, plot a firing trajectory for its weapons. Here, Jameson description of the craft’s “plotting room,” the “most vital spot in the ship,” seems (unsurprisingly, given his naval background) akin to a description of a battleship or aircraft carrier’s combat information center, “the counterpart of the brain”.

Then, his essay gets really interesting, for – in the context of describing the tracks of two spacecraft engaged in combat, as diagrammed in Figure 2 – he postulates about the nature of space-borne rangefinders and target-bearing transmitters, suggesting for the former determining distance – “sounding” by radio waves – and the latter something akin to a thermoscope, or simply put, a device showing changes in temperature, against a given background.

In other words, he seems to have been respectively anticipating both radar, and, what is now known as IRST: Infrared Search and Track.

5) Interestingly, unlike Willy Ley, Jameson is also an advocate of the use of some form of what he dubs “rocket torpedoes” rather than shells, due to the latter’s “advantage of auto-acceleration” and the “ability to build up speed to any desired value after having been launched,” versus the delay inherent to the sequence of events involved in the the actual firing and movement of a shell from a gun. Of course, even assuming the enemy vessel is attacked with “rocket torpedoes”, such devices – in the context and era of Jameson’s article – would have no internal guidance or tracking system of their own, their “flight” path being entirely dependent on course adjustments of the firing platform – “our” spacecraft – itself.

5) Where mentioned, I’ve included conversions of given velocities (“miles per second”) to velocities per hour, in both English and Metric systems, the former in statue miles. These are denoted by brackets. (e.g., [90,000 mph / 144,840 kph]).

As in the post covering Ley’s article, the most notable passages of the text are italicized and in red, like these last twelve words in this sentence. The post concludes with links to a variety of excellent videos covering spacecraft-versus-spacecraft battles, and “space war”, in greater detail, in light of (quite obviously!) contemporary knowledge.

__________

You can read the Wikipedia article about Malcolm Jameson here, while the Internet Speculative Fiction Database compilation of his writing can be found here.

Jameson’s memorial tribute (I guess penned by John W. Campbell, Jr.?) from the July 1945 issue of Astounding, follows:

MALCOLM JAMESON
December 21, 1891 – April 16, 1945

Malcolm Jameson, a man possessed of more shear courage than most of us will ever understand, died April 16, 1945, after an eight-year writing career, initiated when cancer of the throat forced him to give up the more active life he wanted. Any author can tell you that you can’t write good stuff when you’re feeling sick. Jamie never quite understood that – perhaps because he began when he did. X-ray and radium treatment controlled the cancer for a time, but only at a price of permanent severely bad health.

He sold his first story to Astounding in 1938. [“Eviction by Isotherm“, August, 1938.] That was followed by such memorable and sparklingly light stories as “Admiral’s Inspection,” the whole Commander Bullard series, and his many other stories in UNKNOWN WORLDS.

The man who could accomplish that under the conditions imposed on him was not of ordinary mold.

The Commander Bullard series grew out of Jameson’s own experiences as a Lieutenant in the United States Navy from 1916 till his retirement in 1927. He had much to do with the development of modern naval ordnance; his work is fighting in this war, though he himself was not permitted to do so.

He is survived by his wife, his daughter, Corporal Vida Jameson, of the WAC, his son, Major Malcolm Jameson, in the Infantry and now overseas, and his brother, House Jameson, better known as “Mr. Aldrich” of the “Aldrich Family” program.

The Editor.

____________________

You’ll notice that Hubert Rogers’ iconic depiction of a space fleet control center (for E.E. Smith’s “Gray Lensman”) as the cover of the November, 1939 issue of Astounding, appears below. Further down in the post are two interior illustrations – from the November, 1941, and February, 1948 issues of Astounding, in which Rogers created views of the same scene for Smith’s “Second Stage Lensman” and “Children of the Lens”, respectively. (The image of the control center in the 1948 issue was scanned from an original copy, and photoshopifically “niced up” to bring out the details, for this post.) You can view other images of this nature, and more, at my brother blog, WordsEnvisioned.

____________________

And so, on to Malcolm Jameson’s “Space War Tactics” from the month of November, in the year 1939…

SPACE WAR TACTICS

Expanding on Willy Ley’s recent article, Jameson brings out some important details – not the least of which is that a space battle fleet gets one shot at the enemy in months of maneuvering!

By Malcolm Jameson

Illustrated by Malcolm Jameson

Astounding Science Fiction
November, 1939

Ship to Ship Engagement

A working knowledge of the game of chess is a useful adjunct in understanding the art of war. War is not a series of haphazard encounters hut a definite understanding governed by principles that never change, however much the weapons and uniforms and the colors of the flags may. Like chess it is a continuing struggle between two opponents, each trying to estimate the strength of the other and to divine his purposes and most probable objective, and what his next move will be. It is a marauding and movement of forces, a series of threats and feints, of advances and withdrawals, punctuated by sharp conflict as one or the other forces the issue.

As the rules of chess govern the movement of each piece, so does the field of operations in war, whether it is rocky terrain or swampy, the open sea or the cloud-streaked skies, or the vast reaches of space itself. Tactics, and in a measure the weapons, are rigidly determined by the controlling environment.

We can, therefore predict with some assurance the general nature of space warfare, for we already know something of the properties of the void and what characteristics ships that traverse it arc likely to have. With such ships and in such a theater of operations, we have only to apply the principles of warfare developed by men through centuries of strife to arrive at an approximation of the tactics they will use. We can be fairly certain of the kind of weapons and instruments they will have, for the very advent of spaceships is presumptive of continued advance in science along much the same lines we have already come.

There are two great factors in space warfare that will set it off sharply from anything else in human experience, and those two factors will modify fighting-ship types, strategy and tactics profoundly. They are: (a) the extent of space, and (b) the tremendous speed of the vessels.

At the risk of boring those who have already read and thought a good deal about travel in space and who feel that they long ago formed a satisfactory idea of what the limitless reaches of the void are like, I want to dwell a moment on the subject of the vastness of space. It deserves all the emphasis we can give it.

Psychologists assert that it is beyond the capacity of the human mind to conceive of quantities, extents or durations beyond rather close limits. We may nod understandingly at hearing mention of a billion-dollar appropriation, but we grasp the idea solely because we are thinking of those billion dollars as a unit sum of money. If we tried to visualize them as coins we would fail utterly. The mind cannot picture ten hundred thousands of thousands of silver disks. “Many” is the best it can do – there are too many dollars there for one mindful. And so it is with distance.

It has been my good fortune to have traveled extensively; I have crossed oceans as navigator, stepping off the miles made good each day or watching them slide by under the counter. Thus I have a hazy notion of the size of the Earth – it is oppressively huge. What, then, of the two or three million-mile straightaway covered in a single day’s run of a rocket-ship – represented by a quarter-inch pencil mark on the astragator’s chart of the ecliptic? The Earth he left but yesterday had already dwindled to a small bright disk and before the week is over it will be seen only as a brilliant blue star. In that incredibly vast celestial sphere in which lie is floating – stretching as it does without limit before, behind and to every side, above and below – where and how can we hope to find his enemy?

For even if he passed another ship close aboard, he would not so much as glimpse it. Speeds in space are as stupendous as the spaces they traverse. Needing seven miles per second to escape the Earth and another twenty to make any reasonable progress between the planets, even the slowest vessels will have speeds of twenty-five miles per second [90,000 mph / 144,840 kph]. Warships. presumably. according to type, will have correspondingly higher speeds – perhaps as high as fifty miles per second [180,000 mph / 289,682 kph … or, 0.000268 c] for the faster scouts.

Speeds of that order are as baffling to the imagination as the depths of the void. When we recall that the fastest thing most of us are familiar with is the rifle bullet, whizzing along at a lazy half-mile per second [1,800 mph / 2,897 kph], we see that we do have a yardstick. The ships mentioned above proceed at from fifty to one hundred times that fast – invisible, except under very special circumstances. It is barely possible, we know, for a quick eye to pick up twelve-inch shells in flight if he knows just where, when and how to look, but a momentary glimpse is all he gets.

When we talk of gunfire or any other means of offense, we have to bear these dizzy speeds firmly in mind. The conclusion is irresistible that scouting, tracking, range finding and relative bearings will all be observed otherwise than visually. Even on the assumption of attack from the quarter, the most obvious approach – and for the same reason that aviators “get on the tail” – the overtaking vessel must necessarily have such an excess of speed that the visual contact can last but a few seconds. Each of the combatants must compute the other’s course from blind bearings and ranges and lay their guns or point their torpedo tubes by means of a differentia calculator.

However, in this blind tracking there is one peculiarity of these ships that while it is in one sense a source of danger to them, is of distinct assistance. In the fleeting minutes of their contact, neither can appreciably alter course or speed! This is a point that writers of fiction frequently ignore for the sake of vivid action, but nevertheless it is an unavoidable characteristic of the [e]ther-borne [?!] ship.

The human body can withstand only so much acceleration and the momentum these vessels carry has been built up, hour after hour, by piling increment of speed on top of what had been attained before. In space there is no resistance. Once the rockets are cut, the ship will soar on forever at whatever velocity she had at the moment of cutting. Her master may flip her end over end and reverse his acceleration, but his slowing will be as tedious and cautious as his working up to speed. Jets flung out at right angles merely add another slight component to the velocity, checking nothing.

Rocket experts have stated that an acceleration of one hundred feet per second per second can be withstood by a human being – perhaps one hundred and fifty in an emergency. The master of a vessel proceeding at forty miles per second [144,000 mph / 231,745 kph] applying such an acceleration at right angles would succeed in deflecting his flight about one hundred miles by the end of the first minute, during which he will have run twenty-four hundred – a negligible turn, if under fire. Applied as a direct brake, that hundred miles of decreased velocity would slow him by one twenty-fourth – obviously not worth the doing if the emergency is imminent.

With these conditions in mind, let us imagine a light cruiser of the future bowling along at forty miles per second on the trail of an enemy. The enemy is also a cruiser, one that has slipped through our screen and is approaching the earth for a fast raid on our cities. He is already decelerating for his prospective descent and is thought to be about one hundred and fifty thousand miles ahead, proceeding at about thirty-five miles per second [126,000 mph / 202,777 kph]. Our cruiser is closing on him from a little on his port quarter, and trying to pick him up with its direction finders.

So far we have not “seen” him. We only know from enciphered code messages received several days ago from our scouting force, now fifty millions astern of us, that he is up ahead. It would take too long here to explain how the scouts secured the information they sent us. The huge system of expanding spirals along which successive patrols searched the half billion cubic miles of dangerous space lying between us and the enemy planet is much too intricate for brief description. It is sufficient for our purposes that the scouts did detect the passage of the hostile cruiser through their web and that they kept their instruments trained on him long enough to identify his trajectory. Being neither in a position to attack advantageously nor well enough armed – for their function is the securing of information, and that only – they passed the enemy’s coordinates along to us. This information is vital to us, for without it the probability of contact in the void is so remote as to be nonexistent.

The ship in which we are rushing to battle is not a large one. She is a bare hundred meters [328 feet] in length, but highly powered. Her multiple rocket tubes, now cold and dead, are grouped in the stern. We have no desire for more speed, having all that is manageable already, for after the few seconds of our coming brush with the enemy our velocity is such that we will far overrun him and his destination as well. It will require days of maximum deceleration for us to check our flight and be in a position to return to base.

Our ship’s armament, judged by today’s standards, will at first sight appear strangely inadequate. Our most destructive weapon is the “mine,” a simple sphere of meteoric iron about the size of a billiard ball, containing no explosive and not fused. The effectiveness of such mines depends upon the speed with which they are struck by the target ship – no explosive could add much to the damage done by a small lump of iron striking at upward of thirty miles a second. Then there will he torpedo tubes amidships, and perhaps a few guns, but it may lie well to postpone a discussion of the armament until we have examined the conditions at the place of battle.

Although we know in a general way where the enemy is and where he is going, before we close with him we must determine his course and speed very accurately, for our ability to hit him at all is going to depend upon extremely nice calculations. Our speeds are such that angular errors of so much as a second of arc will be fatal, and times must be computed to within hundredths of seconds.

This falls within the province of fire-control, a subject seldom if ever mentioned by fiction writers. There is no blame to be attached to them for that, for the problems of fire-control are essentially those of pure mathematics, and mathematics is notoriously unthrilling to the majority of readers. Yet hitting with guns – or even arrows, though the archer solves his difficulties by intuition – requires the solution of intricate problems involving the future positions and movements of at least two bodies, and nothing more elementary than the differential calculus will do the trick. In these problems interior ballistics, for all its interesting physics, boils down to a single figure – the initial velocity of the projectile, while exterior ballistics evaporates for the most part the moment we propel our missile into a gravityless vacuum. In space we are to be concerned with the swiftly changing relationship of two rapidly moving vessels and the interchange of equally swift projectiles between them, the tracks of all of them being complicated curves and not necessarily lying in a plane.

In its simplest statement the problem of long-range gunnery is this: where will the enemy be when my salvo gets there? For we must remember that even in today’s battles the time the projectile spends en-route to its target is appreciable – fully a minute on occasion, at sea, during which the warship fired upon may move as much as half a mile. Under such circumstances the gunner does not fire directly at his target, but at the place it is going to be. That requires very accurate knowledge of where the enemy is headed and how fast he is moving.

At sea that is done by observing successive bearings and ranges and plotting them as polar coordinates, bearing in mind that the origin is continuously shifting due to the ship’s own motion. This work of tracking – the subsequent range-keeping and prediction of future ranges and bearings – is done in our times in the plotting room. This is the most vital spot in the ship, for if her weapons may be likened to fists and her motive power to legs, her optical and acoustical instruments to eyes and ears, then the plotting room is the counterpart of the brain. There all the information is received, corrected, digested, and distributed throughout the ship. Without that co-ordination and direction the ship would be as helpless as an idiot.

Well, hardly that helpless today. Our individual units, such as turret crews, can struggle on alone, after a fashion. But not so with the ship of the future. There the plotting room is everything, and when it is put out of commission, the ship is blind and paralyzed. It will, of course, be located within the center of the ship, surrounded by an armored shell of its own, and in there will also be the ship control stations.

The best way to approach the problems our descendants will have to face is to consider a simple problem in tracking that our own warships deal with daily. It is an absurdly simple one compared to the warped spirals to be handled in space warfare, but it will serve to illustrate the principle. In Fig. 1. it is shown graphically, but in actual practice the elements of the problem are set up on a motor-driven machine which thereupon continuously and correctly delivers the solutions of problems that would take an Einstein minutes to state. As the situation outside changes, corrections are cranked into the machine, which instantly and uncomplainingly alters its calculations.

In the figure we have the tracks of two ships, ours the left-hand one. For the sake of clarity and emphasis I have made the ratio of speeds three to one, but the same trends would be shown at the more usual ratio of, say, 20:19

At positions “1,” “2,” “3” and so on, we observe the range and hearing of the target, and plot them. By noting the differences between successive readings and the second differences between those, we soon have an idea of the type of curve the rates of changes would plot into. In a short time we can also note that the rates themselves are changing at a certain rate. This is a rough sort of differentiation – by inspection – and to one familiar with such curves these trends have a definite meaning.

For example, it is apparent that the series of observed angles “Beta” are steadily opening, signifying that we are drawing past the target. Any sudden alteration of the second differences, such as occurs at “8,” at once indicates a change of condition on the part of the enemy. He has either turned sharply away or slowed to half speed, for the bearing suddenly opens nearly two degrees more than the predicted beating. We learn which by consulting our ranges. It could be a combination of changed course and changed speed.

The ranges during the first seven lime-intervals have been steadily decreasing, although the rate of decrease has been slowing up, indicating we are approaching the minimum range. At “8,” though, the range not only fails to decrease, but the rate of change actually changes sign. We know without doubt that the enemy has turned away.

The importance of having the machine grind out predicted bearings and ranges, aside from the desirability of speed and accuracy, is that at any moment smoke, a rain squall, or intervening ships may obscure the target. In that event the gunners need never know the difference – their range and bearing indicators arc ticking away like taximeters, fed figures by the controlling range-keeper. It would not have mattered if sight had been lost of the enemy at “4”; the gun- fire would have been just as accurate up to the time he changed course as if they had the target in plain sight, t

As a matter of fact, the guns are not pointed at the target at all, but in advance of it, as is shown in Fig. 1 (a), both range and bearing being altered to allow for the forward movements of the target while the shells are in the air. The projectiles may be regarded as moving objects bandied on a “collision course” with regard to the enemy vessel.

Speaking of collision courses, it is an interesting property of relative bearings that when the bearing remains constant – except in the special case of the vessels being on parallel courses at identical speeds – the vessels will eventually collide, regardless of what their actual courses and speeds are. Hence, from the time the shots of the salvo left their guns – Fig. 1 (a) – until they struck their target, the target bore a constant angle of thirteen degrees to the right of the nose of the shells. (This knowledge has some utility in estimating the penetration of armor at the destination.)

In the example above, all the movement can be regarded as taking place in a plane; the ships follow straight courses and they maintain constant speeds. Our terrestrial problems are in practice much complicated by zigzagging, slowing down and speeding up, but at that they are relatively child’s play compared to what the sky-warrior of the future must contend with.

His tracks are likely to be curved in three dimensions, like pieces of wire hacked out of a spiral bed spring, and whether or not they can be plotted in a plane, they will nowhere be straight. Moreover, whatever changes of speeds occur will be in the form of steady accelerations and not in a succession of flat steps linked by brief accelerations such as we know. Computing collision courses between two continually accelerating bodies is a much trickier piece of mathematical legerdemain than finding the unknown quantities in the family of plane trapeziums shown in Fig. I. Yet projectiles must be given the course and speed necessary to insure collision.

The gunnery officer of the future is further handicapped by rarely ever being permitted a glimpse of his target, certainly not for the purpose of taking ranges and bearings. In the beginning of the approach the distances between the ships is much too great, and by the time they have closed, their relative speed will generally forbid vision.

Since optical instruments are useless except for astrogational purposes, his rangefinders and target-bearing transmitters will have to be something else. For bearings, his most accurate instrument will probably be the thermoscope – an improved heat-detector similar to those used by astronomers in comparing the heat emission of distant stars. It will have a spherical mounting with a delicate micro-vernier. A nearby spaceship is sure to radiate heat, for it is exposed constantly to full sunlight and must rid itself of the excess heat or its crew will die. Once such a source of heat is picked up and identified, it can be followed very closely as to direction, although little can be told of its distance unless something is known of its intrinsic heat radiation.

Ranges will probably be determined by sounding space with radio waves, measuring the time interval to the return of reflected waves. It is doubtful whether this means will have a high degree of accuracy much beyond ranges of one light-second on account of the movement of the two vessels while the wave is in transit both ways. At long range the need for troublesome corrections is sure to enter.

Such observations, used in conjunction with one another, should give fairly accurate information as to the target’s trajectory and how he bears from us and how far he is away. This data will be fed into a tracking and range-keeping machine capable of handling the twisted three-dimensional curves involved, and which will at once indicate the time and distance of the closest point of approach. Both captains will at once begin planning the action. They may also attempt to adjust their courses slightly, but since the rockets evolve great heat, neither can hope to keep his action from the knowledge of the other owing to the sensitiveness of the thermoscopes.

The rangekeeping instrument suggested, while far surpassing in complexity anything we know of today, will represent a much smaller technical advance than the rockets which drive the ships that house them. We already have similar machines, so that their counterparts of the future would seem much less mysterious to us than, say, the Walschaert’s valve gear to Hero or Archimedes, or the Jacquard loom to the weavers of the Gobelin tapestries.

Assuming we have, by observation and plotting, full knowledge of the enemy’s path and have come almost into position to commence the engagement, we find ourselves confronted once more with the two overwhelming factors of space warfare – great distance and immense speeds – but this time in another aspect. We have come up close to our foe – in fact we are within twenty seconds of intersecting his trajectory – and our distance apart is a mere four hundred miles [643 km]. It is when we get to close quarters that the tremendous problems raised by these lightning-like speeds manifest themselves most vividly.

Look at Fig. 2.

The elapsed time from the commencement of the engagement until the end is less than twenty seconds. Our ship is making forty miles per second, the other fellow is doing thirty-three. We will never be closer than fifty miles, even if we regard the curves as drawn as being in the same plane. If one rides over or below the other, that minimum range will be greater. What kind of projectile can cross the two or three hundred miles separating the two converging vessels in time to collide with the enemy? Shooting cannon with velocities as low as a few miles per second would be like sending a squadron of snails out from the curb to intercept an oncoming motorcycle – it would be out of sight in the distance before they were well started.

Projectiles from guns, if they were to be given velocities in the same relation to ships’ speeds that prevail at present, would have to be stepped up to speeds of three to four thousand miles per second! A manifest impossibility. It would be difficult, indeed, to hurl any sort of projectile away from the ship at greater initial velocities than the ship’s own speed. Such impulses, eighty times stronger than the propelling charge of today’s cannon, would cause shocks of incredible violence. It follows from that that an overtaken ship is comparatively helpless – unless she is in a position to drop mines – for whatever missiles she fires have the forward inertia of the parent ship and will therefore be sluggish in their movement in any direction but ahead.

Another difficulty connected with gunfire is the slowness with which it comes into operation. This may seem to some to be a startling statement, but we are dealing here with astonishing speeds. When the firing key of a piece of modern artillery is closed, the gun promptly goes off with a bang. To us that seems to be a practically instantaneous action. Yet careful time studies show the following sequence of events: the primer fires, the powder is ignited and burns, the gases of combustion expand and start the shell moving down the tube. The elapsed time from the “will to fire” to the emergence of the projectile from the muzzle is about one tenth of a second. In Fig. 2 our target will have moved more than three miles while our shell is making its way to the mouth of the cannon! It looks as if guns wouldn’t do.

I come to that conclusion very reluctantly, for I am quite partial to guns as amazingly flexible and reliable weapons, but when we consider that both powders and primers vary somewhat in their time of burning, there is also a variable error of serious proportions added to the above slowness. It is more likely that the rocket-torpedoes suggested by Mr. Willy Ley in a recent article on space war will be the primary weapon of the future. They have the advantage of auto-acceleration and can therefore build up speed to any desired value after having been launched.

The exact moment of their firing would have to be computed by the tracking machine, as no human brain could solve such a problem in the time allowed. But even assuming machine accuracy, great delicacy in tube-laying and micro-timing, the chances of a direct hit cm the target with a single missile is virtually nil. For all their advanced instruments, it is probable that all such attacks will be made in salvos, or continuous barrages, following the time-honored shotgun principle. For the sake of simplicity, only two such salvos are shown on the diagram, but probably they would be as nearly continuous as the firing mechanisms of the tubes would permit. Any reader with a flair for mathematics is invited to compute the trajectories of the torpedoes. The ones shown were fired dead abeam in order to gain distance toward the enemy as rapidly as possible.

It is desirable that these torpedoes should vanish as soon as practicable after having overrun their target. To that end their cases are made of thin magnesium, and between the head and the fuel compartment is a space filled with compressed oxygen and a small bursting charge The tip of the head is loaded with liquid mercury. Such a massive projectile would penetrate any spaceship with ease, but if it missed it would burst as soon as the fuel supply was spent and then consume itself in brilliant flame, thus avoiding littering the Spaceways with dangerous fragments.

Spotting, as we know it, would be impossible, for the target would be invisible. Hits would have to be registered by the thermoscope, utilizing the heat generated by the impact. The gunnery officer could watch the flight of his torpedoes by their fiery wakes, and see his duds burst; that might give him an idea on which side of the enemy they passed in the event the thermoscopes registered no hits.

If there were guns – and they might be carried for stratosphere use – they could be brought into action at about “15,” firing broad on the starboard quarter. The shells, also of self-destroying magnesium, would lose some of their forward velocity and drift along in the wake of the ship while at the same time making some distance toward the oncoming enemy. These guns would be mounted in twin turrets, one on the roof and the other on the keel, cross-connected so that they would be trained and fired together. It the ships center of gravity lay exactly between them, their being fired would not tend to put the ship into a spin in any direction. What little torque there might be, due to inequalities in the firing charge, would be taken care of by the ship’s gyro stabilizer, an instrument also needed on board to furnish a sphere of reference so that the master could keep track of his orientation.

If upon arriving at point “16” the enemy were still full of fight and desperate measures were called for, we could lay down mines. These hard little pellets would be shot out of mine-laying tubes clustered about the main driving jets. They would be shot out at slight angles from the fore-and-aft line, and given a velocity exactly equal to the ship’s speed, so that they would hang motionless where they were dropped. Being cheap and small, they could be laid so thickly that the enemy could not fail to encounter several of them. If she had survived up to this point, the end would come here.

The end, that is, of the cruiser as a fighting unit. Riddled and torn, perhaps a shapeless mass of tangled wreckage, she would go hurtling on by, forever bound to her marauding trajectory. The first duty of our cruiser would be to broadcast warnings to the System, reporting the location of its own mine-field, and giving the direction taken by the shattered derelict. Sweepers would be summoned to collect the mines with powerful electromagnets, while tugs would pursue and clear the sky of the remnants of the defeated Martian.

______________________________

Illustration by Hubert Rogers, for “Second Stage Lensman – Part I“, by Edward E. Smith, PhD., from Astounding Science Fiction, November, 1941, page 35. (Cover also by Rogers.)

____________________

Illustration by Hubert Rogers, for “Children of the Lens – Conclusion“, by Edward E. Smith, PhD., from Astounding Science Fiction, February, 1948, page 122. (Cover by Alejandro Canedo)

______________________________

— References and Related Readings —

Malcolm R. Jameson, at Wikipedia

Malcolm R. Jameson, at International Science Fiction Database

Hubert Rogers, at SciFiGuy

Hubert Rogers, at International Science Fiction Database

Space War, at Atomic Rockets

Vacation in the Golden Age of Science Fiction, by Jamie Todd Rubin

Warfare in Science Fiction, at Technovology

Weapons in Science Fiction, at Technovology

— Here’s a book —

Wysocki, Edward M., Jr., An ASTOUNDING War: Science Fiction and World War II, CreateSpace Independent Publishing Platform, April 16, 2015

— Lots of Cool Videos —

Because Science – Kyle Hill

Why Every Movie Space Battle Is Wrong ((at Nerdist) 5/11/17)

The Truth About Space War (4/12/18)

Curious Droid – Paul Shillito

Electromagnetic Railguns – The U.S Military’s Future Superguns – 200 mile range Mach 7 projectiles (11/4/17)

Will Directed Energy Weapons be the Future? (6/12/20)

Generation Films – Allen Xie

Best Space Navies in Science Fiction (2/10/20)

5 Most Brilliant Battlefield Strategies in Science Fiction (5/8/20)

5 Things Movies Get Wrong About Space Combat (5/12/20)

6 More Things Movies Get Wrong About Space Battles (5/28/20)

Why “The Expanse” Has the Most Realistic Space Combat (6/21/20)

It’s Okay To Be Smart – Joe Hanson

The Physics of Space Battles (9/22/14)

PBS SpaceTime – Matt O’Dowd

The Real Star Wars (7/19/17)

5 Ways to Stop a Killer Asteroid (11/18/15)

Science & Futurism with Isaac Arthur (SFIA) – Isaac Arthur

Space Warfare (11/24/16)

Force Fields (7/27/17)

Interplanetary Warfare (8/31/17)

Interstellar Warfare (3/8/18)

Planetary Assaults & Invasions (5/17/18)

Attack of the Drones (9/13/18)

Battle for The Moon (11/15/18)

The Infographics Show

What If There Was War in Space? (12/23/18)

Railguns and More! – The Battle of Thoth Station, in “The Expanse”

Rocinante Attack on Thoth Station (Episode “Doors & Corners”) “The Expanse”, Season 2, Episode 2 (Air Date 2/1/17), at DailyMotion

List of “The Expanse” Episodes, at Wikipedia

War in Space, 1939 – I: “Space War”, in Astounding Science Fiction, by Willy Ley (August, 1939)

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/emc2ftl3/public_html/wp-includes/formatting.php on line 4365

Deprecated: Function create_function() is deprecated in /home3/emc2ftl3/public_html/wp-content/plugins/wp-spamshield/wp-spamshield.php on line 2033

So.

…lately, I’ve been perusing my collection of science-fiction pulps – Astounding Science Fiction; Analog; Galaxy Science Fiction; The Magazine of Fantasy and Science Fiction; Startling Stories; Beyond Fantasy-Fiction, and more – admiring cover and interior art; acknowledging the enjoyment of paper and ink versus the stale purity of pixels; and especially (especially!) appreciating the contrast between the first time I read “such and such” a story in a paperback anthology – say, Fredric Brown’s “Arena“, in Volume I of The Science Fiction Hall of Fame – versus said story in its original incarnation in the June, 1944 issue of Astounding.

It seems.

…that the very contrast between things; events; images – as we remember them – and as they actually are, can be of deeper and more provocative impact that those very “things” themselves.

And.

…that “contrast” can easily extend to the taken-for-granted realms of ideas or technology. In the of science fiction, striking examples of this – striking, in juxtaposition with the “world” of 2021 – appeared in Astounding Science Fiction in August and November of 1939, in the form of articles by Willy Ley and Malcolm Jameson. Respectively entitled “Space War” and “Space War Tactics”, both authors presented analyses of how battles between spacecraft (emphasizing individual ship-versus-ship combat) would actually be conducted – in the particular and obvious context of the nature of scientific knowledge and the technology of the late 1930s – versus how such conflict then and even in subsequent decades, was imagined. (Or, anticipated?!)

Well.

…I enjoyed reading these articles. And, in light of contemporary and ongoing news about “space” having become a realm of military activity – at a level even beyond what has already transpired since the early 1960s; at a level beyond that of reconnaissance alone – I thought you’d appreciate them, too.

Anyway.

….what I’ve done is fully transcribe both articles as two posts, one article per post – just as they appeared in Astounding back in ’39. These posts include all illustrations and captions that appeared in the original articles, to which I’ve tossed in some videos (you’ll see what they are), links to additional sources of information, and a little information about one author (Malcolm Jameson) in particular. In the Jameson article (in the next post), velocities listed in the text have been recalculated as miles (statue miles) and kilometers per hour.

Purposefully.

…These posts are not primarily intended to critique the technological validity of the analyses and conclusions arrived at by Ley or Jameson. Rather, they’re instead to open a window upon the intellectual, scientific, and even social “flavor” of the times. While some of the authors’ analyses and conclusions will be incorrect, quaint, or utterly passe in light of scientific and technological developments that have occurred during the intervening eighty-two (gad, 82?!) years, I can’t help but wonder about the continuing relevance and validity of at least some of their insights, in terms of general concepts about kinetic – projectile – weapons versus “rays”, or, aspects of identification, tracking, and aiming by opposing spacecraft, in the context of speed, and, other factors. So, each article is preceded by a summary of its central points, with the most notable passages of the text being italicized and in red text, like these last thirteen words in this sentence. Both posts conclude with links to a variety of excellent videos covering spacecraft-versus-spacecraft battles, and “space war”, in greater detail, in light of (quite obviously!) contemporary knowledge.

________________________________________

Here’s Willy Ley’s “Space War” from August of 1939.

Some general “take-aways” from his article are:

1) The technology needed for spacecraft already exists, even in rudimentary form.

2) The possibility exists that civilization will progress to such a point where war will become outlawed. Given ( – alas – ) human nature, in the more likely alternative, the potential and impetus for human conflict that has always existed on earth will continue as man explores space.

3) By definition, space conflict will parallel aerial conflict by being manifested in three dimensions of movement.

4) In literary depictions of space warfare, a literary device and plot element has been that of energy weapons. I think Ley is implying infrared projectors or beam weapons.

However, a weapon far, far more mundane and less dramatic, yet vastly more effective, practical, and solidly within the realm of technological development and practical use is some variant of: The gun. “Well, I still believe that there is no better, more efficient and more deadly weapon for space warfare than an accurate gun with high muzzle velocity. And I believe that an intelligent being from another planet, that is advanced enough to build or at least to understand spaceships, will look like a man – at least to somebody who does not see very well and cannot find his glasses.”

5) The technology envisioned for energy or beam weapons – “ray projectors” – even if these can successfully be developed – is prohibitively heavy, bulky, and impractical for use in spacecraft.

6) Assuming that some form of “gun” is used in space warfare, the projectiles fired by such weapons would be analogous to those used in conventional, “earth-bound” conflicts, albeit specifically relevant to spacecraft versus spacecraft battles. These would be: 1) High explosive thin-walled shells, and 2) Shells containing large numbers of individual non-explosive projectiles.

7) Some science fiction depictions of space warfare rely on the concept of defensive “screens” (perhaps analogous to the use of “shields” in Star Trek?). But, can “screens” of whatever nature – “gravity screens” in particular – be developed in theory, let alone technologically, in light of current and future knowledge about the nature of gravity?

8) Rockets would be a possible weapon in space battles, albeit this being 1939, Ley is discussing unguided rockets. The disadvantages of such weapons are that they could be (relatively) easily spotted, and, the impracticality and danger in storing a relatively large quanitty of combustible and/ or explosive material aboard a spacecraft, let alone the size and mass of such weapons.

9) Space battles would be characterized by craft camouflaged “night-black”, and using any possible measures to reduce their thermal signatures.

10) Paralleling this, ammunition would be used “sparingly” due to the eventual (!) danger of intact ordnance remaining in orbit around the Sun. (Or, any old sun.)

11) It would be absolutely essential that the effects of the recoil of any specific weapon, or more likely combination of weapons located at disparate points on the spacecraft’s hull (think of an analogue to the five gun turrets (four remote-control) of a WW II B-29 Superfortress), on the spacecraft’s trajectory be compensated for by the craft’s main engine, or, maneuvering thrusters.

____________________

Oh, before we start with Ley’s article, a comment about this issue’s cover art: This is the only issue of Astounding Science Fiction for which the cover illustration – for which any illustration, really – was created by Virgil Finlay. Given Finlay’s superb – sometimes astonishing; almost preternatural; in my opinion quite unparalleled – artistic skill, I’d long wondered why an artist of his caliber had no other association with the magazine most central to the development of science fiction as a literary genre.

You can find the answer below, in an excerpt from a vastly larger post (link here) at my brother blog, WordsEnvisioned.

__________

VIRGIL FINLAY – Dean of Science Fiction Artists

by SAM MOSKOWITZ

Worlds of Tomorrow
November, 1965

Except for an unfortunate experience Finlay might have become a regular illustrator for Astounding Science-Fiction, then the field leader.

Street & Smith had launched a companion titled Unknown, to deal predominantly in fantasy. Finlay had been commissioned to do several interior drawings for a novelette The Wisdom of the Ass, which finally appeared in the February, 1940 Unknown as the second in a series of tales based on modern Arabian mythology, written by the erudite wrestler and inventor, Silaki Ali Hassan.

John W. Campbell had come into considerable criticism for the unsatisfactory cover work of Graves Gladney on Astounding Science-Fiction during early 1939. So it was with a note of triumph, in projecting the features of the August, 1939 issue, he announced to his detractors:

“The cover, incidentally, should please some few of you. It’s being done by Virgil Finlay, and illustrates the engine room of a spaceship. Gentlemen, we try to please!”

The cover proved a shocking disappointment. Illustrating Lester del Rey’s The Luck of Ignatz, its crudely drawn wooden human figures depicted operating an uninspired machine would have drawn rebukes from the readers of an amateur science-fiction fan magazine. The infinite detail and photographic intensity which trademarked Finlay was entirely missing.

No one was more sickened than Virgil Finlay. He had been asked to paint a gigantic engine room, in which awesome machinery dwarfed the men with implications of illimitable power. He had done just that; but the art director had taken a couple of square inches of his painting, blown it up to a full-size cover and discarded the rest.

The result was horrendous. A repetition of it would have seriously damaged his reputation, so Finlay refused to draw for Street and Smith again.

____________________

And so, now on to Willy Ley’s article…

SPACE WAR

Suggesting that rays, ray screens, and all super-potent weapons of science-fiction aren’t half as deadly as a weapon we already have.

By Willy Ley

Illustrated by Willy Ley

Astounding Science Fiction
August, 1939

ABOUT ten years ago, Professor Hermann Oberth, the famous rocket expert, made an interesting experiment which, although having to do with rockets, required neither laboratory nor proving ground. It was a legal experiment. Professor Oberth submitted to the German Patent Office a complete description, with drawings, of a “Space Rocket.” It was, virtually, a spaceship with all the details he had been able to think of in many years of study.

After the usual acknowledgment, there was complete silence for some time. Then one day a bulky letter arrived from the patent office, containing the expected rejection. But it was more than just a rejection. Patent offices do not reject things without explaining why. And the staff of the patent office did explain. They had pried the plans apart and patiently and expertly examined every part of them. And after really tremendous research and labor they had arrived at the conclusion that Professor Oberth’s plans could not be patented because every part and device was known to engineering science and had been patented before in some country by somebody else. (1)

The decision, or rather the explanation given, was in a way more valuable than the granting of a patent would have been. It proved that spaceships arc not so far beyond the horizon as most people think – the very conservative and very careful staff of a patent office had found that they existed already – only in parts scattered all over and throughout civilization. Periscopes, air purifiers, air-proof hulls, automatic devices and instruments of all kinds, water regenerators, et cetera, et cetera – they all exist and not even the much-discussed rocket motors are really novel. Devices very similar to those needed on a tremendous scale for spaceships have already been built on a small scale for gas turbines.

It is, of course, true that, in spite of the decision of the patent office, space-ships arc still to be invented. Every one of the thousand and one parts needs special adaptation, re-designing and re-research. There is still a tremendous amount of work to be done, and much has to be “invented.” Point is, however, that there is nothing new in principle that is needed for space travel. It was almost the same story with airplanes forty years ago. Everything needed to build an airplane existed. There was steel tubing and the art of welding it. There were sheet aluminum and rubber. There were wheels and propellers, wings were known and gasoline engines could be bought. The invention of the airplane was delayed because those engines were too weak – it is exactly the same with rocket motors.

With more powerful engines came airplanes. And with airplanes came thoughts of military application. At first only observing was contemplated. Even in actual war – 1914 – airplanes did not combat each other at first. They observed enemy movements were fired at from the ground and retaliated with primitive bombs. But the pilots of two airplanes meeting in the air are said to have saluted each other – flying alone was dangerous enough. Then one day somebody began to shoot with a pistol and soon planes were having machine- gun combats.

It is only logical to assume that space war will follow the advent of the spaceship as aerial warfare followed in the wake of the airplane. Not from the very outset, probably, because the first space-ships will entail sufficient risk of life in themselves. But later spaceships will have means to combat each other in space and one day somebody will find, or create, a reason to use these means. It is possible, though not any too likely, that mankind will have progressed beyond the use of brute force when space travel has advanced to a fair degree of perfection. And if by then war has already been successfully outlawed, there will be space police and blockade runners. There will be combat, even if not war.

So much for the likeliness of battles in space – even without the famous invasion from an alien solar system. How will these battles be fought? New means of transportation bring new kinds of battle tactics. Roman chariots fought in another manner than the horsemen of Dshingis Khan. Byzantine galleys employed other tactics than Sir Francis Drake, and he had other ideas of naval battle than the commander of the U.S.S. Washington.

IN AERIAL BATTLE a new element became important, the maneuverability in three dimensions. It was not the better gun or the faster plane that decided many single engagements, but the Immelmann turn. Evidently space war will develop its own tactics – but tactics depend also to a very great extent on the type of armament in use. That, of course, does not present any question to the science-fiction fan. He knows it by heart from hundreds of stories, the authors of which neither overexerted their imagination nor perceive a need for too much originality. Traditionally spaceships attack each other with heat-ray projectors of incredible temperature and tremendous capacity; they probe into each other’s vitals with searing needle rays. They bombard each other’s screens with proton guns and barytron blasters. They waste energy in appalling quantities, they do anything but shoot.

____________________

Figure 1. Pressure curves the barrels of guns.

____________________

To pull the lanyard of a shiny 75-millimeter nickel-steel gun would be too trivial a thing to do. Just about as trivial, in fact, as to picture a race of bearded men in white silk dresses armed with crossbows on a planet of Beta Draconis. The beings that live there must be walking octopi, waving heat guns and disintegrator pistols in their tentacles. Normal human-looking people would not be hostile enough to the visitors from Terra, and spaceships with simple guns would certainly be ridiculous and puny. Besides, guns would be to no avail against the ultrarefractory super alloys of the spaceships, and the shells would simply be deflected by force fields.

Well, I still believe that there is no better, more efficient and more deadly weapon for space warfare than an accurate gun with high muzzle velocity. And I believe that an intelligent being from another planet, that is advanced enough to build or at least to understand spaceships, will look like a man – at least to somebody who does not see very well and cannot find his glasses.

Before going into detail about the advantages of guns it is advisable to contemplate the relative merits of ray projectors. That they do not exist now is immaterial; science-fiction is not only concerned with things that are but also with those that might be. How would they look if they did exist? They would consist of two main parts, the mechanism that produces and projects the rays and the power plant that feeds said mechanism.

Power plants are notoriously heavy and, even if we assume atomic power, the power generator will not be just a vest-pocket affair. It would probably need a lot of insulation and a powerful cooling device. We can say with certainty that it would be heavy and bulky. Also, it will probably be sensitive against shaking and jarring, and it would be unpleasant indeed to see all the atomic converters go out of action in the middle of a battle. The ray generator itself would most certainly be sensitive since we have to assume tubes of some kind. And these sensitive ray projectors would have to be in the outer hull of the ship – or even outside the outer hull – so that they do not damage the wrong hull.

So much for the “merits” of ray generators. Now the rays themselves. Even the most powerful and most fantastically destructive ray will need some time to inflict damage. Which implies the need for complicated sighting and focusing devices. How well the rays will focus is another question. Almost invariably the beams will spread out with distance. The farther the target is away the weaker the radiation becomes. The weaker it becomes the longer it has to strike. But holding a ray on a fast-moving distant target, that might be practically invisible with black paint against the background of black space, is no small job.

Besides, those rays are supposed to be more than mere searchlights. They are supposed to have unpleasant destructive qualities, being twelve thousand degrees hot, for example. Naturally the generator has to be able to endure its own heat. But, if there is an insulating material that holds out against the energies released at the giving end, it is hard to understand why the same insulator should not be usable to safeguard the hull of the ship that is being rayed – especially since the energy concentration at the receiving end is only a fraction of that at the giving end.

John W. Campbell evaded all these troublesome questions nicely in his “Mightiest Machine” by introducing the transpon beams. These rays are fairly innocent in themselves, but they have the ability of carrying a large variety and an enormous quantity of vicious radiations originating elsewhere and not touching the projectors. It is possible that something like this might be accomplished one day, but ordinary rays, as they are usually featured in science-fiction stories, have no place in actual future space war. Even if they could be generated they would not have any practical military value.

A GUN is a much nicer instrument. It is compact and sturdy, cannot be damaged by anything less potent than a direct hit from another gun, and does not require a special power plant. Compared to what one would have to carry around to produce even feeble rays the weight of a gun is small. Besides, a gun is something we do know how to handle. More than six centuries of continuous use have taught us how to take advantage of the fact that certain mixtures of chemicals burn with utmost rapidity and produce large quantities of gases while doing so.

That fact permits three main types of possible application, every one of them in use in ordinary warfare and fit to be used in space war, too. The large volume of gas that is generated suddenly can either he used to destroy its container and whatever happens to be around – that’s the principle of the bomb. Or it might be discharged comparatively slowly through a hole in the container so that the recoil moves the container – the principle of the rocket. Finally it might be discharged suddenly through a tube which is blocked by a solid movable object that is then blown out vehemently at high speed just like a dart from a blow gun – the principle of the firearm. All three, bomb, rocket and gun, were invented in rapid succession soon after the discovery of gunpowder.

____________________

Figure 2. Three types of explosive shells. Type A is a light, bursting shell, for surface damage. B, heavily cased with armor, is designed to penetrate steel and concrete armor before bursting. C is a sort of “flying machine-gun,” a shrapnel shell to scatter hundreds of deadly pellets as bursting.

__________

Figure 3. Antirecoil device for gases. The explosion gasses, turned backward, tend to kick the rifle forward as hard as the bullet’s recoil kicks it backward.

____________________

The latter was found in China around the year 1200 A.D., certainly not much earlier – the statements of old encyclopedias notwithstanding. Bombs and powder rochets were used for the first time in 1232 during the bottle of Pien-king. They were then “newly invented.” As to guns we think that we even know the exact year of their invention. The Memoriebook (chronicle) of the city of Ghent contains under the year 1313 the entry:

“Item, in dit jaer was aldereerst gevonden in Duitschland het gebruik der bussen van eenen mueninck.” Translation: “By the way, during this year the use of bussen was discovered for the first time by a monk in Germany.”

“Bussen” meaning portable guns. The oldest picture of a gun can be found in an Oxford manuscript, De Officiis Regum, from the year 1326. Eighty years later guns were known in all civilized countries.

But it took more than four centuries until the science of ballistics came into being. A great many other sciences, especially mathematics, had to be developed first before the performance of a gun could be predicted to a certain extent.

Ballistics arc extremely complicated, and it is hard to tell whether interior or exterior ballistics present fewer or lesser headaches. The term “exterior ballistics” applies to the movement of the projectile from the moment it leaves the muzzle of the gun until it hits the target. “Interior ballistics,” consequently means the movement of the projectile within the gun barrel. The principles are simple in both cases.

The distance reached by a projectile is determined by its muzzle velocity that should be as high as possible and by the angle of elevation where 45 degrees represents the optimum. High muzzle velocity is, therefore, the main goal, and the laws of interior ballistics tell how it can best be attained. There are only a few forces at work. The expanding gases that result from the explosion of the driving charge push the projectile ahead of them, the higher the pressure, the faster. And the longer the barrel the more time to push. Counteracting forces are the inertia of the projectile and its friction against the walls of the barrel. It seems, therefore, that the barrel should he very long and very smooth, the pressure very high and the projectile very light.

Unfortunately it is not quite as simple as becomes apparent if we follow the events in a more detailed form. The shot begins with the ignition of the driving charge. It is here where things look most beautiful. One kilogram of ordinary black gunpowder produces 285 liters of gas at the temperature of zero degrees centigrade, the freezing point of water. One kilogram of TNT develops 592 liters, one kilogram of nitroglycerin 713 liters, and one kilogram of nitro-cellulose powder even 990 liters. Now these volumes are valid for zero degrees centigrade. But the gases are hot, their volume increases by about one third of the zero degree volume for each 100° C. rise. And the temperature of combustion is high, about 2000° C. for black powder, 2600° C. for TNT, 3100° C. for nitroglycerin and 2200° C. for nitro-cellulose powder. There is a limit as to what the barrel can stand and don’t forget that it is supposed to have a service life, too. Things are a little easier if the powder burns rapidly but not instantaneously; the reason, incidentally, why only a very few known explosives can be used as driving charges. A short moment after complete combustion of the driving charge the internal pressure reaches its highest point, afterward expansion alone works.

THE LENGTH of a barrel is usually expressed not in inches or centimeters, but in calibers, a word which came from the Arab, where it means “model” (standard). Very short stubby mortar barrels are 12-15 calibers long, heavy naval gun 40-50 calibers and infantry rifles even 90 calibers. They are not smooth but “rifled”, having a spiral groove which forces the projectiles to spin around their longitudinal axes. Artillery shells fit the barrel loosely – the rifle effect and the gas tight fit are accomplished by copper rings laid around the shell.

We have arrived at the point where the gases drive the shell by their expansion only. The speed of the projectile is still increasing then, but not for very long. The infantry rifle 98 [referring to the German Gewehr 98 bolt action rifle?] that was and is in use in a number of European armies and has been investigated very thoroughly, may now serve as an example, its bore is 0.3 inches, the “bullet” weighs 10 grams, the driving charge 3.2 grams. The barrel is 29.1 inches, or about 90 calibers long.

The bullet leaves the muzzle with a velocity of 2936 feet per second, involving a small loss of energy since the muzzle velocity could be 66 feet higher if the barrel were 45-4 inches or 150 calibers long. These figures show how much the friction in the barrel retards the bullet. To attain a speed of 2936 feet per second a barrel length of 90 calibers is required. But an additional length of 60 calibers would increase the muzzle velocity by only 66 feet. No wonder the designers preferred to save these 66 feet, and save weight and material. If the barrel was much longer, the bullet would not leave it. That’s what would happen in the case of rifle 98 if the length of the barrel surpassed 23 feet.

In special cases longer barrels were built: The 80-mile gun that fired at Paris from the forest of Crepy in March, 1918 (2) had a barrel that was 118 feet or 170 calibers long. However, only three quarters of that barrel were rifled, the last 45 calibers of length were smooth. Another retarding factor, not often mentioned and apparently not yet fully determined is the air above the shell in the barrel. Since the projectile acquires supersonic speeds, that air cannot escape but has to be compressed, which might mean a considerable loss in the case of a long gun of large caliber.

Point one in favor of guns in space war: they do not have to spend that energy.

When the projectile leaves the muzzle the trouble really starts. Older books say that the trajectory is a parabola – it is elliptical with the center of the Earth as one of the focal points of the ellipse. The trajectory is influenced by the rotation of the Earth, by the attraction of large mountains, by barometric pressure and by the humidity of the air and by a number of other factors that might be avoided by careful design. Incidentally, streamlining would be useless; we deal with supersonic velocities. While the shell rises the velocity decreases until the peak of the flight is reached. Then the velocity increases again, due to gravitational attraction, and decreases with mounting speed due to increasing air resistance.*

____________________

*Most of these factors become noticeable only in long trajectories. The changes in velocity are beautifully shown in the following table, calculated by Max Valler for the trajectory of the Paris Gun – authentic data are still secret.

angle	distance (km)	altitude (km)	velocity (km/sec)	time (sec)
54	0	0	1.5	0
53	3.45	4.67	1.3	4.2
50	10.83	14.00	1.06	14.3
45	19.70	23.72	.93	27.3
40	26.80	30.33	.86	38.2
25	43.07	41.04	.72	62.1
0	63.34	46.20	.65	94.5
25	83.55	41.60	.71	120.0
40	99.06	31.20	.84	150.5
50	115.99	16.60	.95	173.3
53	122.00	6.12	.94	191.0
58	126.00	0	0.86	199.0

____________________

The main factors are therefore, gravity and resistance – two more points in favor of the use of guns in space. There is no air resistance and the gravitational fields are weak where spaceships usually travel.

That bullet from infantry rifle 98 has near its muzzle 3000 foot pounds of kinetic energy. When it hits a target 3280 feet (1 kilometer) from the muzzle its kinetic energy is only 336 foot pounds, and at 2 kilometers a mere 88 foot pounds. The extreme range of that rifle is about 4 kilometers (2.5 miles), but if there were no air it would carry more than 70 kilometers (43.5 miles). Rifles do not attain more than 5% of their vacuum range under normal surface conditions, field artillery pieces attain about 20%, heavy artillery shells about 25%, long naval rifles of large caliber 30%, and long-range guns up to 50%, because the longer part of their trajectory is situated in the near- vacuum of the stratosphere.

In space in a weak gravitational field, the infantry rifle bullet would arrive at a target 20 miles distant – you could hardly aim without a telescope at something farther away – with about 3020 foot pounds of kinetic energy. No, “3020” is not a printing error, because the muzzle velocity would be higher, due to the lack of air resistance in the barrel!

AFTER being pleased so much with the performance of a portable rifle we’ll have a look at “real” guns. There exists an especially nice field piece, La Soixante-quinze, the famous French 75 millimeter gun. It has a 20-caliber barrel, about 7 feet 4 inches long. Its shell weighs 14.3 pounds, the muzzle velocity in air is 1970 feet per second, the kinetic energy at the muzzle about 2,800,000 foot pounds. [!?]

The barrel of the .75 weighs about 680 pounds, each cartridge about 22 pounds, so that gun, additional equipment and 150 rounds of ammunition amount to about two tons – not excessive a weight for a ship that does not have to carry passengers or cargo – say a Patrol cruiser – but very impressive an armament for a spaceship. Of course, the gun would not be a three-inch field piece. In a French paper on Avions de gros bombardement it was very recently pointed out that guns are much heavier than necessary.

____________________

Figure 4. English war-rocket. This rocket shell is listed in the official British tables of war equipment – a modern, practical rocket shell.

____________________

Designers simply did not pay much attention to weight as long as the gun did not become too heavy for land transport, or if – in case it was too heavy – could be divided into easy loads. Besides, military experts have their ideas about service life. One of my closest friends once designed a new type of compass for a firm working for one of the large European navies. After exhaustive tests that compass was rejected because it was too light! It was later redesigned with parts and casings that were not stronger than the original parts, but multiplied the weight. The weight of gun barrels, to get back to the topic, could be reduced to about half without visibly shortening of service life and it could be reduced to a quarter if a shorter service life would be accepted. That brings even a six-inch long-range gun within reach for large cruisers that do patrol duty; for example, in circling planets. “Six-inch long range,” incidentally, means just that in space, it could shoot at enemies farther away than a portable telescope could show.

So there is certain no need for a special weapon. How about special shells? On Earth three main types are in use: One that dumps as much high explosive as a thin-walled shell will hold on the enemy; one that has to pierce armor and has, therefore, thicker walls and a very strong tip, and one that contains little explosive and many lead balls to scatter around against living targets.

Your first guess is probably that the armor-piercing type is the given projectile for space war. Which raises the question how much armor is to be pierced. Terrestrial field guns are equipped with a shield supposed to protect the gun crew against rifle and machine-gun fire and smaller splinters. Before the World War a shell of 3 millimeters was considered sufficient, but direct rifle fire from distances of a thousand feet or less penetrated them.

____________________

Figure 5. Cross-section of proposed space rocket shell. To get striking power in a rocket equivalent to a 75 shell, the driving charge of the rocket would be inordinately heavy.

____________________

Light battle cruisers on the seas carry a six-inch armor around; it would afford protection against hits from fairly distant 75 mm. guns. However, a six-inch armor is considered light; most warships carry ten-inch armor plate, and the heaviest battle wagons show up to 30 inches of armor. Now a battleship has only an armor belt, protecting the sides where hits are most likely, and protecting those spots where hits would be most destructive. A large section of the ship is protected by the water in which it floats. Spaceships are not so lucky as to have vulnerable points: they are vulnerable all around. Therefore, they need armor plate all over the hull.

The weight of such an armor is a nice example for mathematical enjoyment at breakfast or during a subway ride. We’ll say that a fair-sized spaceship is 90 yards [82.3 meters; 270 feet] long and 20 yards [18.3 meters; 60 feet] in diameter. To make matters easier we shall assume that the shape is cylindrical, to make up for the difference in surface between cylinder and cigar shape we’ll forget about top and bottom of the cylinder and restrict ourselves to the curved surface. That surface is equal to the length of the cylinder, multiplied by the diameter, times pi which makes 5070 square yards. One square yard of six-inch armor plate weighs not quite a ton. Multiplied by the number oi square yards we arrive at, roughly, twelve million pounds!

You can cut down for the thickness of the armor as much as you want. It will always be too heavy, until you arrive at plates of a thickness the outer hull would haw to have anyhow.

In short, a Spaceship cannot be protected by plate armor. Its only defense is its offensive power, since it can always carry guns hundreds of times as powerful as the heaviest possible armor. So we don’t need armor piercing projectiles, any projectile will penetrate the hull – even rifle bullets.

The important difference is that a spaceship cannot be sunk either – a fact not stressed enough by science-fiction authors. When a battleship gets a few really serious holes, it is soon out of action and it is relatively unimportant whether the crew abandons ship or sinks with it firing as long as they are above water. A few bad hits that struck a spaceship may disable it as a means of transportation, but it still does not disappear. If every man wears a spacesuit the loss of air can be temporarily disregarded. The various gun posts can and will continue firing until every man on board is disabled. (3)

Space war, therefore, calls for shells that either blast the enemy to smell pieces at once or for shells that quickly disable every man on board. Which means that either high-explosive shells with thin walls and much H-E are used, or else those shells that contain large numbers of individual bullets should be steel balls and not lead balls, as in terrestrial warfare If the range is short – as “short” ranges in space go – machine guns are not bad at all, or else that nice contraption that goes under the name of “Chicago Piano,” consisting of eight one-pounder rapid-fire guns mounted on one beam, each firing 200 rounds per minute. [QF 2-pounder Mk VIII naval gun, a.k.a. “multiple pom-pom”.] If a spaceship were subjected to the concert of a Chicago Piano for only one minute it would certainly look even worse than after a treatment with heat and disintegrator rays, especially since those rays are usually blocked in stories by adequate screens.

____________________

“An eight gun 2-pounder QF Mk VIII anti-aircraft ‘Pom Pom’ gun installation.” (From History of War.)

____________________

“If a spaceship were subjected to the concert of a Chicago Piano for only one minute it would certainly look even worse than after a treatment with heat and disintegrator rays…”

“The pods, assholes!”

(No other dialogue needed.)

____________________

THOSE screens deserve a short discussion, too. As far as ray screens against hostile rays are concerned, we do not need to worry for long. Without effective rays there is no need for ray screens. But it is another story with those fictive screens that are supposed to offer protection against flying pieces of matter charged with kinetic energy. Could those force fields, or meteorite detectors, or whatever you like to call them be made to actually protect a spaceship? Strong electric or magnetic fields can deflect material bodies, but the influence is much too weak to avail against bullets with supersonic speeds. To create a field of such power and range would require equipment of such a ponderous mass and weight – even assuming atomic power – that nickel-steel armor might be lighter. Only gravity screens would really afford protection.

A gravity screen is supposed to set up a difference in gravity potential and to create what might be called a gravity shadow. A projectile that were to enter a gravity shadow would need as much kinetic energy as is normally required to overcome the difference of gravity potential in question. Since it is also usually assumed that the power of gravity screens can be made to vary, the commander of the ship could “adjust” his screens according to enemy fire.

The trouble with gravity screens is not that we do not know how to make them, but that they cannot be made at all. Devices that “shield off” gravity belong to the category of “permanent impossibilities,” things that cannot be done just as you cannot construct a seven-cornered polygon or trisect a given angle. The problem of the gravity screen has to be regarded as having been solved just as the problem of the perpetuum mobile has been solved: negatively, it cannot be done.

All this applies, however, only to “gravity screens” of the cavorite type and similar marvelous compounds. It does not hold true for what may be termed a “counter field.” Unfortunately we do not know what gravity really is – but it is certainly a force of some kind. If, one day, somebody discovers the truth about gravity he might also find a way to create gravity fields artificially. Now we can conceive of a magnetic field that could eliminate the influence of Earth’s field if the latter were magnetic instead of gravitational. (I am not speaking about Earth’s real magnetic field.)

Similarly we can conceive of a counter field eliminating the effects of the natural gravity fields. To build up a field of the required strength needs lots of power, to be sure, but one might assume that the initial supply could be furnished by a stationary power plant. Such a counter field would, of course, have most of the features of cavorite – among them the protection against projectiles of less kinetic energy than the difference of gravity potentials in question.

With this vague hope for possible protection of spaceships we may safely return to the original topic: means of destruction. Guns and machine guns were found to do nicely – and rocket shells?

Rockets began as weapons of war, they were revived for this purpose by Sir William Congreve in 1804 when there was no other competition for them than smooth-barreled guns of tremendous weight that carried a mile without any accuracy worth mentioning. In fact, Congreve’s rockets and Hale’s later stickless rockets were more accurate than the contemporary guns; hard to believe, but stated in many of the old reports on rocket tests.

And, contrary to popular belief, war rockets were retained in the Service by Great Britain even in the beginning of the twentieth century. The “Treatise on Ammunition,” issued in 1905 [see 1915 edition at Archive.org; see illustrations in 1897 edition at Compass Library] by the (British) War Office, still stated: “Rockets are employed in the service for signaling, for display, as weapons of war, and in conjunction with the life-saving apparatus.” The war rocket officially termed, “Rocket, War, 24-pr., Mark VII, (C). painted red,” was described as being made of steel tubing and cast iron. The average range given was 1800 yards, they had no guiding stick but a device to make them rotate in flight. If these rockets were still used in 1905 or later, they were probably used in colonial service. Despite very many attempts made just at that time to revive war rockets, no army introduced them. Rocket shells behaved, in all the tests that were made, even more erratically in the air than ordinary shells.

It would be different in space. No air resistance would disturb the flight of a rocket-driven shell. And instead of a heavy steel barrel only a thin-walled launched tube would be needed that could even be made of aluminum or magnesium alloys.

The first military objection against rocket shells would be that they could be more easily seen. This, however, could be overcome in using a very high acceleration with short burning period. The driving charge, incidentally, should be powder, not liquids. Powder it not as powerful and not as adaptable as liquid fuel, to be sure, but easier to handle and less expensive because it eliminates the need for mechanisms like combustion chambers, injection nozzles, pressure devices and a host of valves. Powder has the further advantage of having a natural tendency for shorter combustion periods and higher accelerations.

But guns are still superior, this time because of lesser weight!

If the shell part of the rocket shell shall be the same as that of a 75 mm. gun. and if the final velocity of the rocket shell, after complete combustion of the driving charge, shall be equal to that of a gun projectile the comparison of weights looks as follows:

GUN

weight of the gun – 880 pounds
weight of 100 cartridges – 2200 pounds

total weight – 3080 pounds

ROCKETS

launching tube, etc. – 45 pounds
100 shell heads – 1430 pounds
100 rockets with sufficient driving charge – 4300 pounds

total weight – 5775 pounds

Thin, of course, does not mean that rocket shells will not be built. For patrol cruisers guns are better, but other ships will not carry 100 rounds of ammunition all the time, as soon as less than twenty rounds are carried, the rockets are lighter. (There are a few story plots hidden in this statement.) One might conceive of heavy space torpedoes built along the lines of rocket shells, 10 feet long and weighing 1 1/2 tons. But I simply won’t like so much powder in one piece on board – and the construction of such a torpedo with present-day methods of manufacture is, by the way, impossible.

SPACE WAR certainly has its peculiar features, quite different from those pictured in stories, but peculiar just the same. The story picture of shining ships that battle with searing rays and flaming screens is so highly improbable that it can simply be termed wrong. There won’t be any rays and there won’t be screens, especially not the latter because you would be unable to shoot while you had them working.

Instead there would be ships painted night-black, the camouflage of space, carrying guns of incredible range and immensely destructive power. The ships would be extremely vulnerable, but at the same time they could not sink and would be capable of inflicting fatal damage as long as a soul on board is alive.

They would not steam into battle with flying colors, but try to approach unseen with all lights extinguished, avoiding the light background of the Milky Way. If the battle is finally opened ammunition would be used very sparingly, not only because the supply is limited, but because missing is almost as bad as being hit. The 2000-3000 feet per second of muzzle velocity do not count very much as compared with the orbital speed of the planets and all the shells that missed show up again at the point of battle after one or two or three years when they have completed their full orbit around the Sun.

That their own fire throws them off course is another reason for few shots. Each 75 mm. shell, weighing 14.3 pounds and leaving in space the muzzle with a velocity of say 2300 feet per second, produces a recoil of 1000 pounds. And the powder charge, weighing, say, 6.5 pounds, and leaving the muzzle with approximately 6600 feet per second produces another 1300 pounds of recoil. A single shot would naturally not influence the course of a 3000-ton patrol cruiser very much, but during a prolonged battle there will be deflections to be corrected by the rocket motors.

On second thought I take that back. The guns do not have to have a recoil that influences the ship. Several years ago Schneider in Creuzot (France) announced a recoil eliminator, based on the difference in speed between shell and driving gases. Since the gases are between two and three times as fast as the shell, they overtake it as soon as it clears the muzzle. The Schneider-Creuzot device was intended to catch these gases and to deflect them by 180 degrees so that their recoil counteracts that of the shell. The example of the 75 mm. gun has shown that the gases, weighing only 6.5 pounds, produce theoretically 1300 pounds recoil, because they are about three times as fast as the 14.3-pound shell that produces only 1000 pounds of recoil. If all the gases could be caught and deflected a full 180 degrees, the gun barrel would actually jerk forward with each shot. Naturally some of the gas simply follows the shell – but tests have shown that the remaining recoil is very low.

There is one remark I wanted to make all through this article, but up to now 1 did not have an opportunity to do so. What I wanted to say was that there was no talk of armament in Professor Oberth’s patent application.

(1) This decision was entirely in accordance with German patent laws. In other countries a patent might have been granted under the same circumstances.

(2) Usually miscalled “Rig Bertha”: the official name was “Kaiser Wilhelm Gun,” the common name “Paris Gun.” “Big Bertha” was the tame of the mobile 17-inch mortar of Krupps. Both guns were designed by Professor Rausenberger [Fritz Rausenberger].

(3) I recall only one story where this point was stressed. Campbell’s “Mightiest Machine.” The fact is also hinted at in Dr. E.E. Smith’s “Skylark III” during the first encounter with the Fenachrome, but it is not especially emphasized.

— References, Related Readings, and What-Not —

Willy O.O. Ley, at Wikipedia

Virgil W. Finlay, at Wikipedia

Space War, at Atomic Rockets

Warfare in Science Fiction, at Technovology

Weapons in Science Fiction, at Technovology

— Here’s a book —

Wysocki, Edward M., Jr., An ASTOUNDING War: Science Fiction and World War II, CreateSpace Independent Publishing Platform, April 16, 2015

— Lots of Cool Videos —

Because Science – Kyle Hill

Why Every Movie Space Battle Is Wrong ((at Nerdist) 5/11/17)

The Truth About Space War (4/12/18)

Curious Droid – Paul Shillito

Electromagnetic Railguns – The U.S Military’s Future Superguns – 200 mile range Mach 7 projectiles (11/4/17)

Will Directed Energy Weapons be the Future? (6/12/20)

Generation Films – Allen Xie

Best Space Navies in Science Fiction (2/10/20)

5 Most Brilliant Battlefield Strategies in Science Fiction (5/8/20)

5 Things Movies Get Wrong About Space Combat (5/12/20)

6 More Things Movies Get Wrong About Space Battles (5/28/20)

Why “The Expanse” Has the Most Realistic Space Combat (6/21/20)

It’s Okay To Be Smart – Joe Hanson

The Physics of Space Battles (9/22/14)

PBS SpaceTime – Matt O’Dowd

The Real Star Wars (7/19/17)

5 Ways to Stop a Killer Asteroid (11/18/15)

Science & Futurism with Isaac Arthur (SFIA) – Isaac Arthur

Space Warfare (11/24/16)

Force Fields (7/27/17)

Interplanetary Warfare (8/31/17)

Interstellar Warfare (3/8/18)

Planetary Assaults & Invasions (5/17/18)

Attack of the Drones (9/13/18)

Battle for The Moon (11/15/18)

The Infographics Show

What If There Was War in Space? (12/23/18)

Railguns and more! – The Battle of Thoth Station, in “The Expanse”

Rocinante Attack on Thoth Station (Episode “Doors & Corners”) “The Expanse”, Season 2, Episode 2 (Air Date 2/1/17), at DailyMotion

List of “The Expanse” Episodes, at Wikipedia

Art: “The Luck of Ignatz” – Virgil Finlay’s Preliminary cover for Astounding Science Fiction, August, 1939

Artnet

The Age of Science: Computer Memory, in Astounding Science Fiction – February, 1949

The preeminent science-fiction magazine of the mid-twentieth century was Astounding Science Fiction, which rose to prominence under the editorial reign of John W. Campbell, Jr. First published in January 1930 as Astounding Stories of Super Science, the magazine has continued publication under the leadership of several editors and through various title changes, now being known as Analog Science Fiction and Fact.

Though by definition and nature a science fiction publication, Astounding (akin to its post-WW II counterparts and rivals Galaxy Science Fiction, and, The Magazine of Fantasy and Science Fiction (“F&SF”)) also published non-fiction material. Such non-fiction material included leading editorials, book reviews, and letters, as well as articles – typically, one per issue – about some aspect of the sciences. As in any serial publication, the nature of this content reflected the opinions and interests of the magazine’s readers, and, the intellectual and cultural tenor of the times.

A perusal of science articles in Astounding from the late 1940s reveals a focus on aerodynamics, astronomy, atomic energy, chemistry (organic and inorganic), computation, cybernetics, data storage, electronics, meteorology, physics, and rocketry. (Biology it seems, not so much!) Viewed as a whole, these subject areas – in the realm of the “hard sciences” – reflect interests in space travel (but of course!), the frontiers of physics, information technology, and the creation and use of new energy sources.

Let’s take a closer look.

Here are the (non-fiction) science articles that were published in Astounding Science Fiction in 1949:

January: “Modern Calculators” (Digital and analog calculation), by E.L. Locke; pp. 87-106

February: “The Little Blue Cells” (The “Selectron” data storage tube), by J.J. Coupling; pp. 85-99

March: “The Case of the Missing Octane” (Chemistry of petroleum and gasoline), by Arthur Dugan; pp. 102-113 (Great caricatures by Edward Cartier!)

April: “9 F 19” (Hydrocarbons), by Arthur C. Parlett; pp. 46-162

May: “Electrical Mathematicians” (Machine (electronic) calculation), by Lorne MacLaughlan; pp. 93-108

______________________________

June: “The Aphrodite Project” (Determining the mass of the planet Venus), by Philip Latham; pp. 73-84. (Intriguing cover art by Chesley Bonestell.)

______________________________

July: “Talking on Pulses” (Electronic transmission of human speech and other forms of communication), by C. Rudmore; pp. 105-116.

August: “Coded Speech” (Electronic speech; noise reduction), by C. Rudmore; pp. 134-145

September: “Cybernetics” (Review of Norbert Wiener’s book by the same title), by E.L. Locke; pp. 78-87

October – First article: “Chance Remarks” (Communication research), by J.J. Coupling; pp. 104-111

October – Second article: “The Great Floods” (Review of great floods in human history), by L. Sprague de Camp; pp. 112-120

November: “The Time of Your Life” (Time; Determining the length of the earth’s day), by R.S. Richardson; pp. 110-121

December – First article: “Bacterial Time Bomb“, by Arthur Dugan; pp. 93-95

December – Second article: “Science and Pravda“, by Willy Ley; pp. 96-111

Regardless of the topic, a notable aspect of the non-fiction science content of Astounding (likewise for Galaxy and F&SF) is that mathematics – in terms of equations and formulae, let alone Cartesian graphs – was kept to a minimum, if not eschewed altogether. Science articles largely relied upon text to communicate subject material, and often included photographs (especially for issues published during the latter part of the Second World War) and diagrams as supplementary material.

One such example – from February of 1949 – is presented below, in the form of J.J. Coupling’s article “The Little Blue Cells”.

______________________________

This issue features great cover art by Hubert Rogers for Jack Williamson’s (writing under the pen-name “Will Stewart”) serial “Seetee Shock”. The cover symbolizes adventure and defiance in the face of danger, by incorporating a backdrop of warning and admonition (“YOU WERE NOT EVOLVED FOR SPACE”; “BACK ADVENTURER”, and more) around the figure of a space-suited explorer, while cleverly using extremes of light and dark and a sprinkling of stars to connote “outer space”. Like much of Rogers’ best work, symbolism is as important as representation. (You can enjoy more of Rogers’ work at my brother blog, WordsEnvisioned.)

______________________________

Coupling’s article is notable because it addresses a subject frequently addressed by Astounding, with continuing and likely indefinite relevance: recording, storing, preserving, and accessing information – computer memory.

The article focuses on Dr. Jan A. Rajchman’s – then – newly developed “Selectron Tube”, which was developed in the late 1940s at RCA (Radio Corporation of America) and about which extensive and rich literature is readily available, particularly at Charles S. Osborne’s wesbite. As implied and admitted by Coupling’s article, even at the time of the device’s invention there was ambivalence about its long-term economic and technical viability, despite its functionality and innovative design.

An image of a Selectron Tube, from Giorgio Basile’s Lamps & Tubes, is shown below. (Scroll down to end of post for a photograph showing a Selectron Tube in the hands of its inventor, illustrating its relative size.)

Eventually, the initial, 4,096-bit storage capacity Selectron Tube proved to be more difficult to manufacture than anticipated, and the concept was re-designed for a 256-bit storage capacity Tube. To no avail. Both tube designs were superseded by magnetic core memory in the early 1950s.

As for J.J. Coupling? Well…(!)…this was actually the nom de plume of Dr. John R. Pierce, a CalTech educated engineer, who had a long and rich literary career, writing for Astounding, Analog, and other publications. His lengthy oeuvre is listed at The Internet Speculative Fiction Database.

Today, Dr. Pierce’s “The Little Blue Cells” opens a window onto the world of information technology and scientific literature – for the general public – from over six decades gone by. His article, with accompanying illustrations, is presented below.

______________________________

THE LITTLE BLUE CELLS
By J.J. COUPLING

The most acute problem in the design of a robot, a thinking machine, or any of the self-serving devices of science-fiction is memory. We can make the robot’s body, its sensory equipment, its muscles and limbs. But thinking requires association of remembered data; memory is the essential key. So we present the Little Blue Cells!

Most of the robots I have met have been either man-sized androids with positronic brains to match, or huge block-square piles of assorted electrical junk. The small, self-portable models I admire from a distance, but I feel no temptation to speculate about their inner secrets. The workings of the big thinking machines have intrigued me, however. It used to be that I didn’t know whether to believe in them or not. Now, the Bell Laboratories relay computer, the various IBM machines and the Eniac are actually grinding through computations in a manner at once superhuman and subhuman. With the other readers of Astounding I’ve had a sort of inducted tour through the brain cases of these monsters in “Modern Computing Devices” by E.L. Locke. I’m pretty much convinced. It’s beginning to look as if we’ll know the first robot well long before he’s born.

Perhaps some readers of science fiction can look back to the old, unenlightened days and remember a prophetic story called, I believe, “The Thinking Machine.” The inventor of that epoch had first to devise an “electronic language” before he could build his electrical cogitator. The modern thinking machine of the digital computer type comes equipped with a special electronic alphabet and vocabulary if not with a complete language. The alphabet has the characters off and on, or 0 and 1, the digits of the binary system of enumeration, and words must certainly be of the form 1001-110—and so on. We may take it from Mr. Locke that somewhere in the works of our thinking machine information will be transformed into such a series of binary digits, whether it be fed in on paper tape or picked up by an electronic eye or ear. The machine’s most abstruse thought, or its fondest recollection – if such machines eventually come to have emotions – will be stored away as off’s and on’s in the multitudinous blue cells of the device’s memory.

I’m sure that I’m right in describing the memory cells of the machine as multitudinous and little – that is, if it’s a machine of any capabilities at all. To describe them as blue is perhaps guessing against considerable odds, but there are reasons even for this seemingly unlikely prognostication.

The multitudinous part is, I think, obvious. The more memory cells the machine has, the more the machine can store away – learn – the more tables and material it can have on hand, and the more complicated routines it can remember and follow. The human brain, for instance, has around ten billion nerve cells. It may be that each of these can do more than store a single binary digit – a single off or on, or 0 or 1. Even if each nerve cell stored only one digit, that would still make the brain a lot bigger than any computing machine contemplated at present. Present plans for machines actually to be built call for one hundred thousand or so binary digits, or, for only a hundred-thousandth as many storage cells as the brain has nerve cells. Mathematicians like to talk about machines to store one to ten million binary digits, which would still fall short of the least estimated size of the brain by a factor of one thousand to ten thousand. But, if one hundred thousand and ten million both small numbers as far as the human brain is concerned, they’re big numbers when it comes to building a machine, as we can readily see. It is because of the size of such numbers that we know that the memory cells of our thinking machine will have to be small, and, we might add, cheap.

For instance, some present-day computers use relays as memory cells. Now, a good and reliable relay, one good enough to avoid frequent failure even when many thousands of relays are used, costs perhaps two dollars. If we wanted a million cells, the cost of the relays would thus be two million dollars, and this is an unpleasant thought to start with. Further, one would probably mount about a thousand relays on one relay rack, and so there would be a thousand relay racks. These could perhaps be packed into a space of about six thousand square feet – around eighty by eighty feet. Then, there would have to be quite a lot of associated equipment, for more relays would be needed to make a connection to a given memory cell and to utilize the information in it. This would increase the cost and the space occupied a good deal. The thing isn’t physically possible, but it seems an unpromising start if we wish to advance further toward the at least ten sand-fold greater complexity of the human brain.

Fortunately, at just the time it as needed, something better than the relay has come along. That something, the possessor of the little blue cells, is the selectron. It is a vacuum tube which can serve in the place of several thousand relays. It promises to be reliable, small and, dually, at least, cheaper than relays, and in addition it is very much faster – perhaps a thousand-fold. The selectron was invented by an engineer, Dr. Jan A. Rajchman – pronounced Rikeman – for the purpose of making an improved computer and so its appearance at the right time is, after all, no accident. Instead, it is a tribute to Dr. Rajchman’s great inventive ability. Lots of people who worked on computers knew what the problem was, but only he thought of the selectron.

You might wonder how to go about inventing just what is needed, and if Dr. Rajchman’s career can cast any light on this, it’s certainly worth looking into. Did he, for instance, think about computers from his earliest technical infancy? The answer is that he certainly didn’t. I have a copy of his doctoral thesis, “Le Courant Résiduel dans Les Multiplicateurs D’Electrons Electrostatiques,” which tells me that he was born in London in 1911, that he took his degree at Le Ecole Polytechnique Federale, at Zurich and thereafter did research on a radically new type of electrically focused photo-multiplier – see “Universes to Order,” in Astounding for February, 1944. I am not sure how many different problems he has worked on since, but during the war he did do some very high-powered theoretical work on the betatron, as well as some experimental work on the same device. It would seem that the best preparation for inventing is just to become thoroughly competent in things allied to the field in which something new is needed.

What was needed in connects with computers was, as we have said, a memory cell, or, rather, lot, of them. What do these cells have to do? First of all, one must be able to locate a given cell in the memory so as to put information into it or take information out. Then, one must be able to put into the cell the equivalent of a 0 or a 1. One must have this stay there indefinitely, until it is deliberately changed. Finally, one must be able to read off what is stored in the cell; one must be able to tell whether it signifies 0 or 1 without altering what is in the cell. The selectron has these features.

You might be interested in some of the earlier suggestions for using an electron tube as a memory in a computing machine. The electron beam of a cathode ray tube sounds like just the thing for locating a piece of information, for instance. One has merely to deflect it the right amount horizontally and vertically to reach a given spot on the screen of the tube. One wishes, however, to store a particular piece of information in a particular place and then to find that same place again and retrieve that same piece of information. This would mean producing the exact voltages on the deflecting plates when the formation was stored, and that is by no means easy. Further, if the accelerating voltage applied to the tube changes, the deflecting voltage needed to deflect the beam to a given place changes, and this adds difficulty. When we realize further that our memory simply must not make mistakes, we see that there are real objections -to locating and relocating a given spot by simply deflecting an electron beam to it. The selectron has a radically different means for getting electrons to a selected spot – the selectron grid.

The features of the selectron which Dr. Rajchman holds in his hand – page 163 – are illustrated simply in Figure 1. There is a central cathode and around it a concentric accelerating grid. When this grid is made positive with respect to the cathode, a stream of electrons floods the entire selectron grid, the next element beyond the accelerating grid. The selectron grid, is made up of a number of thin bars located in a circular array, pointing radially outward, and a number of thin rings, spaced the same distance apart as are the bars. Figure 2 shows a portion of the selectron grid formed by the rings and bars. The rings and bars together form a number of little rectangular openings or windows.

Now, in operation each bar and ring of the selectron grid is held either several hundred volts positive with respect to the cathode, or else a little negative with respect to the cathode. After a definite pattern of ages has been established on the selectron grid, the accelerating grid is made positive and the selectron grid is flooded with electrons. What happens? Let us consider first the bars of the selectron grid. Figure 3 tells the story. If two neighboring bars are negative, the approaching electrons are simply repelled and turned back. If an electron enters the space between a positive bar and a negative bar, it is so strongly attracted toward the positive bar that it strikes it and is lost. Only if the bars on both sides of the space which the electron enters are positive does the electron get through. At the rings, the story is the same; an electron can pass between two rings only if both are positive; it is stopped if either one or both are negative. Thus we conclude that electrons can pass through a little window formed by two bars and two rings only if both bars and both rings are positive. If both bars and both rings forming a window are held positive, the window is open; if one or more of the bars or rings are negative, the window is closed. Thus, we have a means for letting electrons through one window at a time.

In the early model selectrons there were sixty-four apertures between bars around the tube, and sixty-four apertures lengthwise, giving four thousand ninety-six windows in all, and any one of these could be selected for the passage of electrons by applying proper voltages to the bars and rings. Does this mean that we must have one hundred twenty-eight leads into the tube for this alone, one for each bar and one for each ring? The tube would certainly work if it had one hundred twenty-eight leads to the selectron grid, but Dr. Rajchman’s ingenuity has cut this down instead to thirty-two, a saving by a factor of four. How is this done? The table of Figure 4 tells the story. Here we have in the top row the numbers of the bars, in order, sixty-four in all. These bars are connected to two sets of eight leads. The second and third rows show to which lead of a given set a bar is connected. Thus, Bar 1 is connected to Lead 1 of Set I. Bar 2 is connected to Lead 1 of Set II, while Bar 64 is connected to Lead 8 of Set II. To save space, some of the bars have been omitted from the table.

You will observe that if we make Lead 7 of Set I positive, and all the rest of the leads of Set I negative, Bars 13, 29, 45 and 61 will be positive. Then, if we make Lead 2 of Set II positive and all the other leads of Set II negative Bars 4, 8, 12 and 16 will be positive. All the bars which do not appear in either of the above listings will be negative. Now, the only adjacent bars listed are 12 and 13, which have been written in italics. Hence, when Lead 7 of Set I and Lead 2 of Set II are made positive and all the other leads negative, electrons can pass between the two adjacent positive bars 12 and 13, but not between any other bars. Thus, by selecting one lead from Set I and one lead from Set II, we can select any of the sixty-four spaces between bars.

The thoughtful reader will have noticed, by the way, that there are only sixty-three spaces between sixty-four bars. This, however, omits the space out to infinity from Bar 1 and back from infinity to Bar 64. We can in effect shorten this space by adding an extra bar beyond the sixty-fourth and connecting it to Bar 1.

The same sort of connection used with the bars is made to the ring so that by selecting and making positive one lead each in two sets of eight leads we can select any of the sixty-four spaces between rings. Thus, in the end we have four sets of eight leads each, two sets the bars and two for the rings. We make positive one wire in each set at a time. The number of possible combinations we can get this way is four thousand ninety-six, and each allows electrons to go through just one window out of the four thousand ninety-six formed by the bars and rings of the selectron grid. The action is entirely positive. A given window is physically located in a given place. Small fluctuations in the voltages applied to the bars and rings will not interfere with the desired operation. This is a lot different from trying to locate a given spot by waving an electron beam around.

The selectron grid and its action are- of course, only a part of the mysteries of the selectron. They provide a means for directing a stream of electrons through one of several thousand little apertures at will. But, how can this stream of electrons be used in storing a signal and then in reading it off again? Part of the answer is not new. For some time electronic experts have n thinking of storing a signal on an insulating surface as an electric charge deposited on the surface by means of an electron stream. Thus, by putting electrons on a sheet of mica, for instance, we can make the surface negative, and by taking them off we can make it positive. It is easy enough to do either of these things, as we shall see in a moment.

There are two very serious difficulties with, such a scheme, however. First, how shall we keep the positive or negative charge on the insulating surface indefinitely? It will inevitably tend to leak off. Second, how can we determine whether the surface is charged positively or negatively without disturbing the charge? The logical exploring tool is an electron beam, but won’t the beam drain the charge off in the charge off in the very act of exploration? Both of these difficulties are overcome in the selectron. To understand how, we must know a little about secondary emission.

Beyond the accelerating and selectron grids of the selectron, as shown in Figure 1, there is a sheet of mica indicated as “storage surface.” This has a conducting backing. We are interested in what happens when electrons pass through an open window in the selectron grid – one made up of four positive bars and rings – and strike the mica. The essential ingredients of the situation are illustrated in the simplified drawing of Figure 5. Here the accelerating grid and the selectron grid are lumped together and shown as positive with respect to the cathode. Electrons are accelerated from the cathode, pass through the accelerating grid and the open window of the selectron grid, and shoot toward the mica storage surface. What happens? That depends on the potential of the storage surface with respect to the cathode.

In Figure 6 the current reaching the part of the storage surface behind an open window is plotted vs. the potential of that part of the storage surface with respect to the cathode. Potential is negative with respect to the cathode to the left of the vertical axis and positive with respect to the cathode to the right of the vertical axis. Current to the storage surface is negative – electrons reaching the surface and sticking below the horizontal axis and positive – more electrons leaving the surface than reaching it – above the horizontal axis. The curve shows how current to the surface varies as the potential of the surface is varied.

If the surface is negative with respect to the cathode, the electrons shot toward it are turned back before they reach it and the current to the surface is zero. If the surface is just a little positive, the electrons shot toward it are slowed down by the retarding field between the very positive selectron grid and the much less positive storage surface, and they strike the surface feebly and stick, constituting a negative-current flow to the surface, and tending to make the surface more negative. If the potential of the storage surface is a little more positive with respect to the cathode, the electrons reach it with enough energy to knock a few electrons out of it. These are whisked away to the more positive selectron grid. These negative electrons leaving the surface are equivalent to a positive current to the surface. There are now as many electrons striking as before, but there are also some leaving, and there is less net negative current to the surface. Finally, at some potential labeled V₀ in Figure 6, one secondary electron is driven from the surface for each primary electron which strikes it, and the net current to the surface is zero. If the potential of the storage surface is higher than V₀, each primary electron releases more than one secondary and there is a net flow of electrons away from the surface, equivalent to a positive current to the surface. This tends to make the storage surface more positive.

As the potential of the storage surface rises further above V₀, current for a time becomes more and more positive. Then, abruptly the neighborhood of the potential V_S of the selectron grid itself, the current becomes negative again and stays negative. Why is this? The the primary electrons still strike the storage surface energetically and drive out more than one electron each. The fact is that these secondary electrons leave the surface with very little speed. When the storage surface is more positive than the selectron grid, there is a retarding field at the storage surface which tends to turn the secondaries back toward the storage surface. Hence, there, is still a flow of primaries – a negative current – to the surface, but the secondaries are turned back before reaching the selectron grid and fall on the storage surface again. Thus, the current to the storage surface is again negative.

Our mechanism for holding the storage surface positive or negative is immediately apparent from Figure 6. If the surface is more positive than Vs, the current to it is negative and its potential will tend to fall. If the surface has a potential between V₀ and Vs, the current to it is positive and its potential will tend to rise. Hence, if the storage surface initially has any potential higher than V₀, current will flow to it in such a way as to tend to make its potential VB, the potential of the selectron grid. If, on the other hand, the potential is between O and V₀, the current to the surface will be negative and the potential of the surface will tend to fall to O. If the potential of the surface is negative with respect to the cathode – less than O – there is no current to it from the electron stream and hence no tendency for the potential to rise and fall. Actually, some leakage would probably result in 3 very slight tendency for the potential to rise.

We see, then, that when it is bombarded by electrons, a part of the storage surface tends naturally to assume one of two potentials, or V_S O. If it has initially any other potential, it tends to come back to one of these. Which potential it assumes is determined by whether the initial potential is greater or less than V₀. Thus, if we store information on the part of the storage surface behind a particular window by making this area have a potential Vs with respect to the cathode – meaning, say, 1 – or O – meaning, O – and if this potential changes a little through electrical leakage, perhaps adjacent portions at a different potential, we can recover or regenerate the original potential merely by opening the window of the selectron grid and flooding the area with electrons. In fact, we can periodically regenerate the potentials behind all windows by opening all windows at once and flooding the whole surface with electrons. This is what is done in the operation of the selectron, and this regenerative feature, which makes it possible to retain the stored information indefinitely despite electrical leakage, is one of the most ingenious and important features of the selectron.

How do we get the information on the portions of the storage surface beind the various windows? That is, how do we initially bring some portions of the surface to the potential Vs and others to the potential V₀? In this process of writing inflation into the tube, we first open the particular one of the four thousand ninety-six windows behind which we wish to store a particular piece of information, thus flooding a little portion of the surface with electrons. Then, to the terminals T of Figure 5, between the cathode and the conducting backstage of the storage surface, we apply a very sharply rising positive pulse, shown as the dashed line of Figure 7. Because of the capacitance between this backing plate and the front of the storage surface, where the electrons fall, this drives the front of the storage surface positive. Then the pulse applied to the conducting backing falls slowly to zero, as shown. However, the action of the electrons falling on the surface tends to make it assume the potential Vs, and so if the pulse falls off slowly enough the portion of the surface on which electrons fall is left at the potential Vs, as shown by the solid line of Figure 7. Application of the pulse will leave the portion of the storage surface behind the open window at the potential Vs regardless of whether its initial potential is Vs or O, and the pulse will not affect portions of the surface behind closed windows, because no electrons reach them.

This tells us how we can bring any selected area of the storage surface to the potential Vs which, we can say, corresponds to writing 1 in a particular cell of this memory tube. By flooding a given area or cell with electrons and applying a sharply falling, negative pulse, which rises again gradually toward O – the dashed pulse of Figure 7 upside down – we can bring any selected area of the storage surface to O potential, and thus write O in any selected cell of the memory.

Thus, each little area of the storage surface behind each window of the selectron grid is a cell of our memory. By opening a particular window – through making one lead of each of the four sets of eight selectron grid leads positive – and pulsing the conducting backing positive or negative, we can make the little area of the storage surface behind that window assume a potential Vs or a potential O, and so can, in effect, write 1 or 0 in that particular memory cell. By opening all windows periodically and flooding all areas with electrons, we can periodically bring all little areas back to their proper potentials, either V_S or O, despite leakage of electrons to or away from the little areas. We can, that is, put thousands of pieces of information into the selectron and keep them there. What about reading? How can we get this information out?

Imagine that the entire inner storage surface is covered with a phosphor or fluorescent material like that used on cathode-ray tube screens or inside of fluorescent lights. Now, suppose we open one window of the selectron, shooting electrons at a particular area of the surface. If that area has a potential O, the electrons will be repelled from it. But, if that area has a potential Vs, corresponding to 1, the electrons will strike the fluorescent surface vigorously, emitting a glow of blue light. Suppose we let this light fall on a photo-multiplier, of the type Dr. Rajchman worked on earlier in his career. Then, when we open a given window of the selectron, if the potential of the surface behind the window is O, we get nothing out of the multiplier. But, if the potential is Vs, there is a flash of light, and a pulse of current from the multiplier. And so, we can not only write a O or a 1 in each little memory cell of the selectron, we can not only keep this information there indefinitely, but we can also read it off at will.

Dr. Rajchman has devised other ways for reading the stored information in the selectron, but the use of a phosphor-coated storage surface together with a photo-multiplier has been one of the preferred method. I have spoken of the phosphor as one giving blue light. This is because the photo-multiplier is more sensitive to blue light than to other colors. And so, I predicted that the memory cells of the thinking machines will be not only multitudinous and small, but also blue.

Of course the selectron provides only a part of the thinking machine – that is, the memory. Associated with it there must be circuits in tubes to seek out stored in tubes to seek out stored information, to make use of it to obtain new formation, to write in that new information, and to make use of the new information in turn. All is a field apart. Still, there is one wrinkle which is so intimately connected with the use of the selectron that it deserves mention here. I have referred to the O or 1 a cell of the selectron which can tore a binary digit or, alternately, as a letter of the electronic alphabet which the machine understands. Now, usually we don’t want to store isolated digits or letters: we want to store complete numbers or words – combinations of 1 and O, as, 10011. This is 19 in binary notation, and might in some instance stand for the nineteenth word in a dictionary. When we look up a number or a word, we want it all at once, not piecemeal.

When we want to write many multi-digit numbers in a book, as, in a table of logarithms, for instance, we usually assign a vertical column for each digit to be stored, and write each digit of a given number in a different column, along the same row. Thus, entries in a log table appear as in Figure 8. Suppose that in using the selectron we assign a different tube to each binary digit of the numbers to be stored. If we wish to store twenty-digit numbers, we will need twenty tubes. Each tube will, in effect, be a given column of our storage space. The different cells in a tube will represent different rows. Thus, Cell 1 of Tube 1 will be Row 1 Column 1, Cell 1 of Tube 2 will be Row 1 Column 2, while Cell 10 of Tube 1 will be Row 10 Column 1, et cetera.

We want to look up all the digits in a given row at once. This means that we want to open corresponding windows in all the tubes at once, and so we can connect the corresponding selectron grid leads of all twenty tubes together. Thus, if want to store a number in Row 1, we apply voltages to the selectron grid leads which will open Window 1 in all tubes. We are then ready to read the number in Row 1 or to write a new number in. The twenty photo-multipliers which read the twenty selectrons are not connected in parallel, but are connected separately to carry off the twenty digits of the number in Row 1 to their proper destinations. Perhaps these twenty leads from the twenty photo-multipliers may go to the twenty backing plates of another twenty selectrons to which it is desired to transfer the number. We see, thus, how a whole table of numbers can be stored in twenty selectrons. The windows 1, 2, 3 et cetera, can represent, for instance, the angle of which we want the sine. The first selectron can store the first digits of all the sines, the second selectron can store all the second digits, et cetera. The twenty digits of the sine of any angle – any window number – can be read off simultaneously from the photo-multipliers of the twenty selectrons.

The selectron isn’t perfect by any means. Perhaps it’s not even the final answer. At the moment, in its early form, it may be almost expensive as relays, but that’s partly because it’s new. It’s certainly great deal more compact than relays, a very great deal faster, and probably more reliable as well. It represents a first huge stride in the electronics of the thinking machine. Just how far it takes us is up to a lot of mathematicians, a lot of circuit gadgeteers, and, especially, to Dr. Jan A. Rajchman and RCA, to whom we must look for smaller, cheaper and better selectrons.

– J.J. Coupling, 1949 –

______________________________

References

Dr. Jan A. Rajchman

Jan A. Rajchman (at Wikipedia)

Jan. A. Rajchman (at I.E.E.E. History)

J.J. Coupling (Dr. John R. Pierce)

J.J. Coupling (at Wikipedia)

J.J. Coupling (at Speculative Fiction Database)

Machine Hearing and the Legacy of John R. Pierce (at Cal Tech) (at CalTech.edu)

Creative Thinking, by John R. Pierce (at Tom Schneider’s “Molecular Information Theory and The Theory of Molecular Machines”)

Selectron Tube

Pierce, John R. (as J.J. Coupling), “The Little Blue Cells”, Astounding Science Fiction, 1949, Vol. 42, No. 6, February, 1949, pp. 85-99

Lamps & Tubes / Lampen & Röhren (Giorgio Basile’s website)

Selectron Tube (at Wikipedia)

RCA Selectron (at Charles Osborne’s “RCA Selectron.com” – superb and comprehensive website)

Почему фон Нейман верил в SELECTRON (“Pochemu fon Neyman Veril v Selectron”) (Why Von Neumann believed in the Selectron) (In Cyrillic)

Astounding Science Fiction

Analog Science Fiction and Fact (at Wikipedia)

Imagining the Integrated Circuit: Astounding Science Fiction – July, 1948

Sometimes, fiction can foresee fact.

Sometimes, entertainment can anticipate reality.

This has long been so in the realm of science fiction, a striking example of which – perhaps arising from equal measures and intuition and imagination – appearing in Astounding Science Fiction in mid-1949. That year, Eric Frank Russell’s three-part serial “Dreadful Sanctuary” was serialized in the June, July, and August issues of the magazine.

(Astounding Science Fiction, June, 1948; cover by William F. Timmins. Note Timmins’ name on the “puzzle piece” in the lower left corner!)

(Astounding Science Fiction, July, 1948; cover by Chesley Bonestell)

With interior illustrations by William F. Timmins, the story, set in 1972, is centered upon the efforts of protagonist John J. Armstrong – an iconoclastic combination of entrepreneur, inventor, and unintended detective – to accomplish the first successful manned lunar landing (as his entirely private venture) in the face the inexplicable mid-flight destruction of each of his organization’s spacecraft. Armstrong doesn’t fit the cultural stereotype of inventor or scientist. As characterized by Russell, “Armstrong was a big, tweedy man, burly, broad-shouldered and a heavy punisher of thick-soled shoes. His thinking had a deliberate, ponderous quality. He got places with the same unracy, deceptive speed as a railroad locomotive, but was less noisy.”

While Russell’s story commences as a solid – and solidly intriguing – mystery, effectively conveying a sense wonder; with characters who portend to be more than two-dimensional; the events, plot, and underlying tone gradually change. With the installments in the magazine’s July and and August issues, what had been a story with an eerie undertone of Fortean inexplicability, technical conjecture (such as the “ipsophone”, a video-telephone imbued with aspects of artificial intelligence – cool! – we’re talking 1948!), and a well-crafted mood of impending threat, gradually and steadily falls flat. A pity, because to the extent that the story succeeds – and in parts it does succeed, and creatively at that – it does so far more as a hard-boiled (and very ham-fisted) detective tale than science-fiction.

Regardless of the story’s literary quality (I don’t think it’s ever been anthologized) the physical and psychological presence of the aptly named Armstrong (“arm”?! “strong”?!) remain consistent throughout. Iconoclastic and independent, he’s extremely intelligent, and if need be, a man capable of brute intimidation, self-defense, and violence. He is also canny, cunning, and psychologically astute.

It is these latter qualities that lead to Armstrong’s discovery – after meeting with a police captain – of a most intriguing device, at his residence in the suburbs of New York City.

Correctly suspicious of surveillance by adversaries, on reaching his residence, “…Armstrong cautiously locked himself in, gave the place the once-over.

“Knowing the microphone was there, it didn’t take him long to find it though its discovery proved far more difficult than he’d expected.

“Its hiding place was ingenious enough – a one hundred watt bulb had been extracted from his reading lamp, another and more peculiar bulb fitted in its place.

“It was not until he removed the lamp’s parchment shade that the substitution became apparent.

“Twisting the bulb out of its socket, he examined it keenly.

“It had a dual coiled-coil filament which lit up in normal manner, but its glass envelope was only half the usual size and its plastic base twice the accepted length.

“He smashed the bulb in the fireplace, cracked open the plastic base with the heel of his shoe.

“Splitting wide, the base revealed a closely packed mass of components so extremely tiny that their construction and assembling must have been done under magnification – a highly-skilled watchmaker’s job! The main wires feeding the camouflaging filament ran past either side of this midget apparatus, making no direct connection therewith, but a shiny, spider-thread inductance not as long as a pin was coiled around one wire and derived power from it.

Illustration by William Timmins (July, 1948, p. 101)

“Since there was no external wiring connecting this strange junk with a distant earpiece, and since its Lilliputian output could hardly be impressed upon and extracted from the power mains, there was nothing for it than to presume that it was some sort of screwy converter which turned audio-frequencies into radio or other unimaginable frequencies picked up by listening apparatus fairly close to hand.

“Without subjecting it to laboratory tests, its extreme range was sheer guesswork, but Armstrong was willing to concede it two hundred yards.

“So microscopic was the lay-out that he could examine it only with difficulty, but he could discern enough to decide that this was no tiny but simple transmitter recognizable in terms of Earthly practice.

“The little there was of it appeared outlandish, for its thermionic control was a splinter of flame-specked crystal, resembling pin-fire opal, around which the midget components were clustered.” (July, 1948, pp.116-117)

I’ll not explain the origin of this device (it’d spoil the story should you read it!), but suffice to say that in the world of the “Dreadful Sanctuary”, things and people are not as they seem, in terms of origin, nature, and purpose.

In our world, however, it seems that Eric Frank Russell created a literary illustration – at least in terms of its diminutive size and the delicacy of its fabrication – of what would in only a few years be known as the integrated circuit.

Sometimes, imagination can anticipate the future.

References

Chesley Bonestell (at Wikipedia)

Eric Frank Russell (at Wikipedia)

William F. Timmins (at Pulp Artists)

Astounding (Analog Science Fiction and Fact)

Integrated Circuit (at Wikipedia)