Deprecated: Function create_function() is deprecated in /home3/emc2ftl3/public_html/wp-content/plugins/wp-spamshield/wp-spamshield.php on line 2033
Three months after the appearance of Willy Ley’s article “Space War” in the August, 1939 issue of Astounding Science Fiction, Malcolm Jameson penned (well, in all probability, he typed – remember typewriters?) a follow-up article of similar length and concept, but focused on a different aspect of spacecraft-to-spacecraft combat: The actual tactics of battle. Thus, Jameson – perhaps reflective of his background as a naval officer – accords attention to the maneuvers utilized by opposing spacecraft, only later in his article discussing weapons, and unlike Ley, being an advocate of “rocket torpedoes”.
Jameson’s article is supplemented by two diagrams which illustrate the trajectories of opposing spacecraft engaged in combat. (You can see his signature at the lower right in each.) In both diagrams – here limited to two dimensions, and viewed from “below” – the track of “our” spacecraft is on the left, and the enemy ship to the right.
In the first diagram, our craft is on a straight trajectory, with the enemy ship taking an abrupt “right” turn at position “7”, the weapons employed by our spacecraft presumably being rocket-torpedoes.
In the second diagram, the pair of spacecraft are on a converging trajectory, the weapons being mines as well as rocket-torpedoes.
Paralleling my post about Willy Ley’s article about space war, here are some general “take-aways” from Jameson’s article:
1) Military conflicts, regardless of the era or the nature of weapons employed, can be expected to follow the same general principles. Thus, though “space” is by nature a setting different from arenas of battle in the traditional sense, the same concepts and assumptions can be expected to hold there, as well.
However, two primary differences stand out: “Space” differs from taken-for-granted terrestrial settings (any planetary setting, really) in terms of its (apparently limitless) extent, and, the speed of the craft involved. The implications and challenges of the latter, in terms of even the nominal possibility of maneuver, as well as locating, tracking, aiming, and firing at enemy craft, cannot be underestimated.
2) Given the speed of combat between spacecraft, gunnery computations (like Willy Ley’s August article, Jameson’s analysis is based on the assumption that spacecraft armament will comprise some form of weaponry firing either simple mass weapons or explosive projectiles, rather than an energy weapon of unknown design and function) will demand the use of a “differentia calculator”. Though he does not elaborate, Jameson seems to have been either anticipating or conceptualizing such a device as ENIAC (Electronic Numerical Integrator and Computer), the existence of which was announced to the public ten months after his death.
3) The spacecraft’s armament is simple, whether by the standards of the late ‘thirties or 2021: The craft shoots projectiles comprised of “a simple sphere of meteoric iron”. Due to the velocities involved, explosives are entirely unnecessary: The momentum of such a projectile is entirely adequate to damage or destroy an enemy spacecraft.
4) A substantial portion of Jameson’s text – specifically pertaining to Figure 1 – pertains to the manner in which “our” spacecraft will locate, identify, and track the enemy vessel, and, plot a firing trajectory for its weapons. Here, Jameson description of the craft’s “plotting room,” the “most vital spot in the ship,” seems (unsurprisingly, given his naval background) akin to a description of a battleship or aircraft carrier’s combat information center, “the counterpart of the brain”.
Then, his essay gets really interesting, for – in the context of describing the tracks of two spacecraft engaged in combat, as diagrammed in Figure 2 – he postulates about the nature of space-borne rangefinders and target-bearing transmitters, suggesting for the former determining distance – “sounding” by radio waves – and the latter something akin to a thermoscope, or simply put, a device showing changes in temperature, against a given background.
In other words, he seems to have been respectively anticipating both radar, and, what is now known as IRST: Infrared Search and Track.
5) Interestingly, unlike Willy Ley, Jameson is also an advocate of the use of some form of what he dubs “rocket torpedoes” rather than shells, due to the latter’s “advantage of auto-acceleration” and the “ability to build up speed to any desired value after having been launched,” versus the delay inherent to the sequence of events involved in the the actual firing and movement of a shell from a gun. Of course, even assuming the enemy vessel is attacked with “rocket torpedoes”, such devices – in the context and era of Jameson’s article – would have no internal guidance or tracking system of their own, their “flight” path being entirely dependent on course adjustments of the firing platform – “our” spacecraft – itself.
5) Where mentioned, I’ve included conversions of given velocities (“miles per second”) to velocities per hour, in both English and Metric systems, the former in statue miles. These are denoted by brackets. (e.g., [90,000 mph / 144,840 kph]).
As in the post covering Ley’s article, the most notable passages of the text are italicized and in red, like these last twelve words in this sentence. The post concludes with links to a variety of excellent videos covering spacecraft-versus-spacecraft battles, and “space war”, in greater detail, in light of (quite obviously!) contemporary knowledge.
__________
You can read the Wikipedia article about Malcolm Jameson here, while the Internet Speculative Fiction Database compilation of his writing can be found here.
Jameson’s memorial tribute (I guess penned by John W. Campbell, Jr.?) from the July 1945 issue of Astounding, follows:
MALCOLM JAMESON
December 21, 1891 – April 16, 1945
Malcolm Jameson, a man possessed of more shear courage than most of us will ever understand, died April 16, 1945, after an eight-year writing career, initiated when cancer of the throat forced him to give up the more active life he wanted. Any author can tell you that you can’t write good stuff when you’re feeling sick. Jamie never quite understood that – perhaps because he began when he did. X-ray and radium treatment controlled the cancer for a time, but only at a price of permanent severely bad health.
He sold his first story to Astounding in 1938. [“Eviction by Isotherm“, August, 1938.] That was followed by such memorable and sparklingly light stories as “Admiral’s Inspection,” the whole Commander Bullard series, and his many other stories in UNKNOWN WORLDS.
The man who could accomplish that under the conditions imposed on him was not of ordinary mold.
The Commander Bullard series grew out of Jameson’s own experiences as a Lieutenant in the United States Navy from 1916 till his retirement in 1927. He had much to do with the development of modern naval ordnance; his work is fighting in this war, though he himself was not permitted to do so.
He is survived by his wife, his daughter, Corporal Vida Jameson, of the WAC, his son, Major Malcolm Jameson, in the Infantry and now overseas, and his brother, House Jameson, better known as “Mr. Aldrich” of the “Aldrich Family” program.
The Editor.
____________________
You’ll notice that Hubert Rogers’ iconic depiction of a space fleet control center (for E.E. Smith’s “Gray Lensman”) as the cover of the November, 1939 issue of Astounding, appears below. Further down in the post are two interior illustrations – from the November, 1941, and February, 1948 issues of Astounding, in which Rogers created views of the same scene for Smith’s “Second Stage Lensman” and “Children of the Lens”, respectively. (The image of the control center in the 1948 issue was scanned from an original copy, and photoshopifically “niced up” to bring out the details, for this post.) You can view other images of this nature, and more, at my brother blog, WordsEnvisioned.
____________________
And so, on to Malcolm Jameson’s “Space War Tactics” from the month of November, in the year 1939…
SPACE WAR TACTICS
Expanding on Willy Ley’s recent article, Jameson brings out some important details – not the least of which is that a space battle fleet gets one shot at the enemy in months of maneuvering!
By Malcolm Jameson
Illustrated by Malcolm Jameson
Astounding Science Fiction
November, 1939
I.
Ship to Ship Engagement
A working knowledge of the game of chess is a useful adjunct in understanding the art of war. War is not a series of haphazard encounters hut a definite understanding governed by principles that never change, however much the weapons and uniforms and the colors of the flags may. Like chess it is a continuing struggle between two opponents, each trying to estimate the strength of the other and to divine his purposes and most probable objective, and what his next move will be. It is a marauding and movement of forces, a series of threats and feints, of advances and withdrawals, punctuated by sharp conflict as one or the other forces the issue.
As the rules of chess govern the movement of each piece, so does the field of operations in war, whether it is rocky terrain or swampy, the open sea or the cloud-streaked skies, or the vast reaches of space itself. Tactics, and in a measure the weapons, are rigidly determined by the controlling environment.
We can, therefore predict with some assurance the general nature of space warfare, for we already know something of the properties of the void and what characteristics ships that traverse it arc likely to have. With such ships and in such a theater of operations, we have only to apply the principles of warfare developed by men through centuries of strife to arrive at an approximation of the tactics they will use. We can be fairly certain of the kind of weapons and instruments they will have, for the very advent of spaceships is presumptive of continued advance in science along much the same lines we have already come.
There are two great factors in space warfare that will set it off sharply from anything else in human experience, and those two factors will modify fighting-ship types, strategy and tactics profoundly. They are: (a) the extent of space, and (b) the tremendous speed of the vessels.
At the risk of boring those who have already read and thought a good deal about travel in space and who feel that they long ago formed a satisfactory idea of what the limitless reaches of the void are like, I want to dwell a moment on the subject of the vastness of space. It deserves all the emphasis we can give it.
Psychologists assert that it is beyond the capacity of the human mind to conceive of quantities, extents or durations beyond rather close limits. We may nod understandingly at hearing mention of a billion-dollar appropriation, but we grasp the idea solely because we are thinking of those billion dollars as a unit sum of money. If we tried to visualize them as coins we would fail utterly. The mind cannot picture ten hundred thousands of thousands of silver disks. “Many” is the best it can do – there are too many dollars there for one mindful. And so it is with distance.
It has been my good fortune to have traveled extensively; I have crossed oceans as navigator, stepping off the miles made good each day or watching them slide by under the counter. Thus I have a hazy notion of the size of the Earth – it is oppressively huge. What, then, of the two or three million-mile straightaway covered in a single day’s run of a rocket-ship – represented by a quarter-inch pencil mark on the astragator’s chart of the ecliptic? The Earth he left but yesterday had already dwindled to a small bright disk and before the week is over it will be seen only as a brilliant blue star. In that incredibly vast celestial sphere in which lie is floating – stretching as it does without limit before, behind and to every side, above and below – where and how can we hope to find his enemy?
For even if he passed another ship close aboard, he would not so much as glimpse it. Speeds in space are as stupendous as the spaces they traverse. Needing seven miles per second to escape the Earth and another twenty to make any reasonable progress between the planets, even the slowest vessels will have speeds of twenty-five miles per second [90,000 mph / 144,840 kph]. Warships. presumably. according to type, will have correspondingly higher speeds – perhaps as high as fifty miles per second [180,000 mph / 289,682 kph … or, 0.000268 c] for the faster scouts.
Speeds of that order are as baffling to the imagination as the depths of the void. When we recall that the fastest thing most of us are familiar with is the rifle bullet, whizzing along at a lazy half-mile per second [1,800 mph / 2,897 kph], we see that we do have a yardstick. The ships mentioned above proceed at from fifty to one hundred times that fast – invisible, except under very special circumstances. It is barely possible, we know, for a quick eye to pick up twelve-inch shells in flight if he knows just where, when and how to look, but a momentary glimpse is all he gets.
When we talk of gunfire or any other means of offense, we have to bear these dizzy speeds firmly in mind. The conclusion is irresistible that scouting, tracking, range finding and relative bearings will all be observed otherwise than visually. Even on the assumption of attack from the quarter, the most obvious approach – and for the same reason that aviators “get on the tail” – the overtaking vessel must necessarily have such an excess of speed that the visual contact can last but a few seconds. Each of the combatants must compute the other’s course from blind bearings and ranges and lay their guns or point their torpedo tubes by means of a differentia calculator.
However, in this blind tracking there is one peculiarity of these ships that while it is in one sense a source of danger to them, is of distinct assistance. In the fleeting minutes of their contact, neither can appreciably alter course or speed! This is a point that writers of fiction frequently ignore for the sake of vivid action, but nevertheless it is an unavoidable characteristic of the [e]ther-borne [?!] ship.
The human body can withstand only so much acceleration and the momentum these vessels carry has been built up, hour after hour, by piling increment of speed on top of what had been attained before. In space there is no resistance. Once the rockets are cut, the ship will soar on forever at whatever velocity she had at the moment of cutting. Her master may flip her end over end and reverse his acceleration, but his slowing will be as tedious and cautious as his working up to speed. Jets flung out at right angles merely add another slight component to the velocity, checking nothing.
Rocket experts have stated that an acceleration of one hundred feet per second per second can be withstood by a human being – perhaps one hundred and fifty in an emergency. The master of a vessel proceeding at forty miles per second [144,000 mph / 231,745 kph] applying such an acceleration at right angles would succeed in deflecting his flight about one hundred miles by the end of the first minute, during which he will have run twenty-four hundred – a negligible turn, if under fire. Applied as a direct brake, that hundred miles of decreased velocity would slow him by one twenty-fourth – obviously not worth the doing if the emergency is imminent.
With these conditions in mind, let us imagine a light cruiser of the future bowling along at forty miles per second on the trail of an enemy. The enemy is also a cruiser, one that has slipped through our screen and is approaching the earth for a fast raid on our cities. He is already decelerating for his prospective descent and is thought to be about one hundred and fifty thousand miles ahead, proceeding at about thirty-five miles per second [126,000 mph / 202,777 kph]. Our cruiser is closing on him from a little on his port quarter, and trying to pick him up with its direction finders.
So far we have not “seen” him. We only know from enciphered code messages received several days ago from our scouting force, now fifty millions astern of us, that he is up ahead. It would take too long here to explain how the scouts secured the information they sent us. The huge system of expanding spirals along which successive patrols searched the half billion cubic miles of dangerous space lying between us and the enemy planet is much too intricate for brief description. It is sufficient for our purposes that the scouts did detect the passage of the hostile cruiser through their web and that they kept their instruments trained on him long enough to identify his trajectory. Being neither in a position to attack advantageously nor well enough armed – for their function is the securing of information, and that only – they passed the enemy’s coordinates along to us. This information is vital to us, for without it the probability of contact in the void is so remote as to be nonexistent.
The ship in which we are rushing to battle is not a large one. She is a bare hundred meters [328 feet] in length, but highly powered. Her multiple rocket tubes, now cold and dead, are grouped in the stern. We have no desire for more speed, having all that is manageable already, for after the few seconds of our coming brush with the enemy our velocity is such that we will far overrun him and his destination as well. It will require days of maximum deceleration for us to check our flight and be in a position to return to base.
Our ship’s armament, judged by today’s standards, will at first sight appear strangely inadequate. Our most destructive weapon is the “mine,” a simple sphere of meteoric iron about the size of a billiard ball, containing no explosive and not fused. The effectiveness of such mines depends upon the speed with which they are struck by the target ship – no explosive could add much to the damage done by a small lump of iron striking at upward of thirty miles a second. Then there will he torpedo tubes amidships, and perhaps a few guns, but it may lie well to postpone a discussion of the armament until we have examined the conditions at the place of battle.
Although we know in a general way where the enemy is and where he is going, before we close with him we must determine his course and speed very accurately, for our ability to hit him at all is going to depend upon extremely nice calculations. Our speeds are such that angular errors of so much as a second of arc will be fatal, and times must be computed to within hundredths of seconds.
This falls within the province of fire-control, a subject seldom if ever mentioned by fiction writers. There is no blame to be attached to them for that, for the problems of fire-control are essentially those of pure mathematics, and mathematics is notoriously unthrilling to the majority of readers. Yet hitting with guns – or even arrows, though the archer solves his difficulties by intuition – requires the solution of intricate problems involving the future positions and movements of at least two bodies, and nothing more elementary than the differential calculus will do the trick. In these problems interior ballistics, for all its interesting physics, boils down to a single figure – the initial velocity of the projectile, while exterior ballistics evaporates for the most part the moment we propel our missile into a gravityless vacuum. In space we are to be concerned with the swiftly changing relationship of two rapidly moving vessels and the interchange of equally swift projectiles between them, the tracks of all of them being complicated curves and not necessarily lying in a plane.
In its simplest statement the problem of long-range gunnery is this: where will the enemy be when my salvo gets there? For we must remember that even in today’s battles the time the projectile spends en-route to its target is appreciable – fully a minute on occasion, at sea, during which the warship fired upon may move as much as half a mile. Under such circumstances the gunner does not fire directly at his target, but at the place it is going to be. That requires very accurate knowledge of where the enemy is headed and how fast he is moving.
At sea that is done by observing successive bearings and ranges and plotting them as polar coordinates, bearing in mind that the origin is continuously shifting due to the ship’s own motion. This work of tracking – the subsequent range-keeping and prediction of future ranges and bearings – is done in our times in the plotting room. This is the most vital spot in the ship, for if her weapons may be likened to fists and her motive power to legs, her optical and acoustical instruments to eyes and ears, then the plotting room is the counterpart of the brain. There all the information is received, corrected, digested, and distributed throughout the ship. Without that co-ordination and direction the ship would be as helpless as an idiot.
Well, hardly that helpless today. Our individual units, such as turret crews, can struggle on alone, after a fashion. But not so with the ship of the future. There the plotting room is everything, and when it is put out of commission, the ship is blind and paralyzed. It will, of course, be located within the center of the ship, surrounded by an armored shell of its own, and in there will also be the ship control stations.
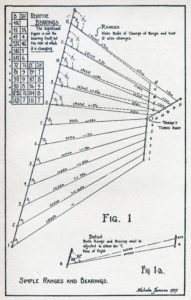
The best way to approach the problems our descendants will have to face is to consider a simple problem in tracking that our own warships deal with daily. It is an absurdly simple one compared to the warped spirals to be handled in space warfare, but it will serve to illustrate the principle. In Fig. 1. it is shown graphically, but in actual practice the elements of the problem are set up on a motor-driven machine which thereupon continuously and correctly delivers the solutions of problems that would take an Einstein minutes to state. As the situation outside changes, corrections are cranked into the machine, which instantly and uncomplainingly alters its calculations.
In the figure we have the tracks of two ships, ours the left-hand one. For the sake of clarity and emphasis I have made the ratio of speeds three to one, but the same trends would be shown at the more usual ratio of, say, 20:19
At positions “1,” “2,” “3” and so on, we observe the range and hearing of the target, and plot them. By noting the differences between successive readings and the second differences between those, we soon have an idea of the type of curve the rates of changes would plot into. In a short time we can also note that the rates themselves are changing at a certain rate. This is a rough sort of differentiation – by inspection – and to one familiar with such curves these trends have a definite meaning.
For example, it is apparent that the series of observed angles “Beta” are steadily opening, signifying that we are drawing past the target. Any sudden alteration of the second differences, such as occurs at “8,” at once indicates a change of condition on the part of the enemy. He has either turned sharply away or slowed to half speed, for the bearing suddenly opens nearly two degrees more than the predicted beating. We learn which by consulting our ranges. It could be a combination of changed course and changed speed.
The ranges during the first seven lime-intervals have been steadily decreasing, although the rate of decrease has been slowing up, indicating we are approaching the minimum range. At “8,” though, the range not only fails to decrease, but the rate of change actually changes sign. We know without doubt that the enemy has turned away.
The importance of having the machine grind out predicted bearings and ranges, aside from the desirability of speed and accuracy, is that at any moment smoke, a rain squall, or intervening ships may obscure the target. In that event the gunners need never know the difference – their range and bearing indicators arc ticking away like taximeters, fed figures by the controlling range-keeper. It would not have mattered if sight had been lost of the enemy at “4”; the gun- fire would have been just as accurate up to the time he changed course as if they had the target in plain sight, t
As a matter of fact, the guns are not pointed at the target at all, but in advance of it, as is shown in Fig. 1 (a), both range and bearing being altered to allow for the forward movements of the target while the shells are in the air. The projectiles may be regarded as moving objects bandied on a “collision course” with regard to the enemy vessel.
Speaking of collision courses, it is an interesting property of relative bearings that when the bearing remains constant – except in the special case of the vessels being on parallel courses at identical speeds – the vessels will eventually collide, regardless of what their actual courses and speeds are. Hence, from the time the shots of the salvo left their guns – Fig. 1 (a) – until they struck their target, the target bore a constant angle of thirteen degrees to the right of the nose of the shells. (This knowledge has some utility in estimating the penetration of armor at the destination.)
In the example above, all the movement can be regarded as taking place in a plane; the ships follow straight courses and they maintain constant speeds. Our terrestrial problems are in practice much complicated by zigzagging, slowing down and speeding up, but at that they are relatively child’s play compared to what the sky-warrior of the future must contend with.
His tracks are likely to be curved in three dimensions, like pieces of wire hacked out of a spiral bed spring, and whether or not they can be plotted in a plane, they will nowhere be straight. Moreover, whatever changes of speeds occur will be in the form of steady accelerations and not in a succession of flat steps linked by brief accelerations such as we know. Computing collision courses between two continually accelerating bodies is a much trickier piece of mathematical legerdemain than finding the unknown quantities in the family of plane trapeziums shown in Fig. I. Yet projectiles must be given the course and speed necessary to insure collision.
The gunnery officer of the future is further handicapped by rarely ever being permitted a glimpse of his target, certainly not for the purpose of taking ranges and bearings. In the beginning of the approach the distances between the ships is much too great, and by the time they have closed, their relative speed will generally forbid vision.
Since optical instruments are useless except for astrogational purposes, his rangefinders and target-bearing transmitters will have to be something else. For bearings, his most accurate instrument will probably be the thermoscope – an improved heat-detector similar to those used by astronomers in comparing the heat emission of distant stars. It will have a spherical mounting with a delicate micro-vernier. A nearby spaceship is sure to radiate heat, for it is exposed constantly to full sunlight and must rid itself of the excess heat or its crew will die. Once such a source of heat is picked up and identified, it can be followed very closely as to direction, although little can be told of its distance unless something is known of its intrinsic heat radiation.
Ranges will probably be determined by sounding space with radio waves, measuring the time interval to the return of reflected waves. It is doubtful whether this means will have a high degree of accuracy much beyond ranges of one light-second on account of the movement of the two vessels while the wave is in transit both ways. At long range the need for troublesome corrections is sure to enter.
Such observations, used in conjunction with one another, should give fairly accurate information as to the target’s trajectory and how he bears from us and how far he is away. This data will be fed into a tracking and range-keeping machine capable of handling the twisted three-dimensional curves involved, and which will at once indicate the time and distance of the closest point of approach. Both captains will at once begin planning the action. They may also attempt to adjust their courses slightly, but since the rockets evolve great heat, neither can hope to keep his action from the knowledge of the other owing to the sensitiveness of the thermoscopes.
The rangekeeping instrument suggested, while far surpassing in complexity anything we know of today, will represent a much smaller technical advance than the rockets which drive the ships that house them. We already have similar machines, so that their counterparts of the future would seem much less mysterious to us than, say, the Walschaert’s valve gear to Hero or Archimedes, or the Jacquard loom to the weavers of the Gobelin tapestries.
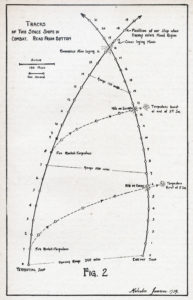
Assuming we have, by observation and plotting, full knowledge of the enemy’s path and have come almost into position to commence the engagement, we find ourselves confronted once more with the two overwhelming factors of space warfare – great distance and immense speeds – but this time in another aspect. We have come up close to our foe – in fact we are within twenty seconds of intersecting his trajectory – and our distance apart is a mere four hundred miles [643 km]. It is when we get to close quarters that the tremendous problems raised by these lightning-like speeds manifest themselves most vividly.
Look at Fig. 2.
The elapsed time from the commencement of the engagement until the end is less than twenty seconds. Our ship is making forty miles per second, the other fellow is doing thirty-three. We will never be closer than fifty miles, even if we regard the curves as drawn as being in the same plane. If one rides over or below the other, that minimum range will be greater. What kind of projectile can cross the two or three hundred miles separating the two converging vessels in time to collide with the enemy? Shooting cannon with velocities as low as a few miles per second would be like sending a squadron of snails out from the curb to intercept an oncoming motorcycle – it would be out of sight in the distance before they were well started.
Projectiles from guns, if they were to be given velocities in the same relation to ships’ speeds that prevail at present, would have to be stepped up to speeds of three to four thousand miles per second! A manifest impossibility. It would be difficult, indeed, to hurl any sort of projectile away from the ship at greater initial velocities than the ship’s own speed. Such impulses, eighty times stronger than the propelling charge of today’s cannon, would cause shocks of incredible violence. It follows from that that an overtaken ship is comparatively helpless – unless she is in a position to drop mines – for whatever missiles she fires have the forward inertia of the parent ship and will therefore be sluggish in their movement in any direction but ahead.
Another difficulty connected with gunfire is the slowness with which it comes into operation. This may seem to some to be a startling statement, but we are dealing here with astonishing speeds. When the firing key of a piece of modern artillery is closed, the gun promptly goes off with a bang. To us that seems to be a practically instantaneous action. Yet careful time studies show the following sequence of events: the primer fires, the powder is ignited and burns, the gases of combustion expand and start the shell moving down the tube. The elapsed time from the “will to fire” to the emergence of the projectile from the muzzle is about one tenth of a second. In Fig. 2 our target will have moved more than three miles while our shell is making its way to the mouth of the cannon! It looks as if guns wouldn’t do.
I come to that conclusion very reluctantly, for I am quite partial to guns as amazingly flexible and reliable weapons, but when we consider that both powders and primers vary somewhat in their time of burning, there is also a variable error of serious proportions added to the above slowness. It is more likely that the rocket-torpedoes suggested by Mr. Willy Ley in a recent article on space war will be the primary weapon of the future. They have the advantage of auto-acceleration and can therefore build up speed to any desired value after having been launched.
The exact moment of their firing would have to be computed by the tracking machine, as no human brain could solve such a problem in the time allowed. But even assuming machine accuracy, great delicacy in tube-laying and micro-timing, the chances of a direct hit cm the target with a single missile is virtually nil. For all their advanced instruments, it is probable that all such attacks will be made in salvos, or continuous barrages, following the time-honored shotgun principle. For the sake of simplicity, only two such salvos are shown on the diagram, but probably they would be as nearly continuous as the firing mechanisms of the tubes would permit. Any reader with a flair for mathematics is invited to compute the trajectories of the torpedoes. The ones shown were fired dead abeam in order to gain distance toward the enemy as rapidly as possible.
It is desirable that these torpedoes should vanish as soon as practicable after having overrun their target. To that end their cases are made of thin magnesium, and between the head and the fuel compartment is a space filled with compressed oxygen and a small bursting charge The tip of the head is loaded with liquid mercury. Such a massive projectile would penetrate any spaceship with ease, but if it missed it would burst as soon as the fuel supply was spent and then consume itself in brilliant flame, thus avoiding littering the Spaceways with dangerous fragments.
Spotting, as we know it, would be impossible, for the target would be invisible. Hits would have to be registered by the thermoscope, utilizing the heat generated by the impact. The gunnery officer could watch the flight of his torpedoes by their fiery wakes, and see his duds burst; that might give him an idea on which side of the enemy they passed in the event the thermoscopes registered no hits.
If there were guns – and they might be carried for stratosphere use – they could be brought into action at about “15,” firing broad on the starboard quarter. The shells, also of self-destroying magnesium, would lose some of their forward velocity and drift along in the wake of the ship while at the same time making some distance toward the oncoming enemy. These guns would be mounted in twin turrets, one on the roof and the other on the keel, cross-connected so that they would be trained and fired together. It the ships center of gravity lay exactly between them, their being fired would not tend to put the ship into a spin in any direction. What little torque there might be, due to inequalities in the firing charge, would be taken care of by the ship’s gyro stabilizer, an instrument also needed on board to furnish a sphere of reference so that the master could keep track of his orientation.
If upon arriving at point “16” the enemy were still full of fight and desperate measures were called for, we could lay down mines. These hard little pellets would be shot out of mine-laying tubes clustered about the main driving jets. They would be shot out at slight angles from the fore-and-aft line, and given a velocity exactly equal to the ship’s speed, so that they would hang motionless where they were dropped. Being cheap and small, they could be laid so thickly that the enemy could not fail to encounter several of them. If she had survived up to this point, the end would come here.
The end, that is, of the cruiser as a fighting unit. Riddled and torn, perhaps a shapeless mass of tangled wreckage, she would go hurtling on by, forever bound to her marauding trajectory. The first duty of our cruiser would be to broadcast warnings to the System, reporting the location of its own mine-field, and giving the direction taken by the shattered derelict. Sweepers would be summoned to collect the mines with powerful electromagnets, while tugs would pursue and clear the sky of the remnants of the defeated Martian.
______________________________
 Illustration by Hubert Rogers, for “Second Stage Lensman – Part I“, by Edward E. Smith, PhD., from Astounding Science Fiction, November, 1941, page 35. (Cover also by Rogers.)
Illustration by Hubert Rogers, for “Second Stage Lensman – Part I“, by Edward E. Smith, PhD., from Astounding Science Fiction, November, 1941, page 35. (Cover also by Rogers.)
____________________
Illustration by Hubert Rogers, for “Children of the Lens – Conclusion“, by Edward E. Smith, PhD., from Astounding Science Fiction, February, 1948, page 122. (Cover by Alejandro Canedo)
______________________________
— References and Related Readings —
Malcolm R. Jameson, at Wikipedia
Malcolm R. Jameson, at International Science Fiction Database
Hubert Rogers, at SciFiGuy
Hubert Rogers, at International Science Fiction Database
Space War, at Atomic Rockets
Vacation in the Golden Age of Science Fiction, by Jamie Todd Rubin
Warfare in Science Fiction, at Technovology
Weapons in Science Fiction, at Technovology
— Here’s a book —
Wysocki, Edward M., Jr., An ASTOUNDING War: Science Fiction and World War II, CreateSpace Independent Publishing Platform, April 16, 2015
— Lots of Cool Videos —
Why Every Movie Space Battle Is Wrong ((at Nerdist) 5/11/17)
The Truth About Space War (4/12/18)
Electromagnetic Railguns – The U.S Military’s Future Superguns – 200 mile range Mach 7 projectiles (11/4/17)
Will Directed Energy Weapons be the Future? (6/12/20)
Best Space Navies in Science Fiction (2/10/20)
5 Most Brilliant Battlefield Strategies in Science Fiction (5/8/20)
5 Things Movies Get Wrong About Space Combat (5/12/20)
6 More Things Movies Get Wrong About Space Battles (5/28/20)
Why “The Expanse” Has the Most Realistic Space Combat (6/21/20)
It’s Okay To Be Smart – Joe Hanson
The Physics of Space Battles (9/22/14)
The Real Star Wars (7/19/17)
5 Ways to Stop a Killer Asteroid (11/18/15)
Science & Futurism with Isaac Arthur (SFIA) – Isaac Arthur
Space Warfare (11/24/16)
Force Fields (7/27/17)
Interplanetary Warfare (8/31/17)
Interstellar Warfare (3/8/18)
Planetary Assaults & Invasions (5/17/18)
Attack of the Drones (9/13/18)
Battle for The Moon (11/15/18)
What If There Was War in Space? (12/23/18)
Railguns and More! – The Battle of Thoth Station, in “The Expanse”
Rocinante Attack on Thoth Station (Episode “Doors & Corners”) “The Expanse”, Season 2, Episode 2 (Air Date 2/1/17), at DailyMotion
List of “The Expanse” Episodes, at Wikipedia